Menu
Math Lesson 4.3.6 - Graph of Inverse Proportion
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
Welcome to our Math lesson on Graph of Inverse Proportion, this is the sixth lesson of our suite of math lessons covering the topic of Proportion, you can find links to the other lessons within this tutorial and access additional Math learning resources below this lesson.
Graph of Inverse Proportion
From the above example, we have demonstrated that two quantities involved in an inverse proportion have a relation of type a × b = constant, which we can write as
or
The graph of this relation is called hyperbola, it is a curved line that approaches the axes without touching them with the increase in the values of a and b. To increase the accuracy of an inverse proportion graph, we must use as many points as possible. Thus, if we reconsider the above example, we can form the following table:
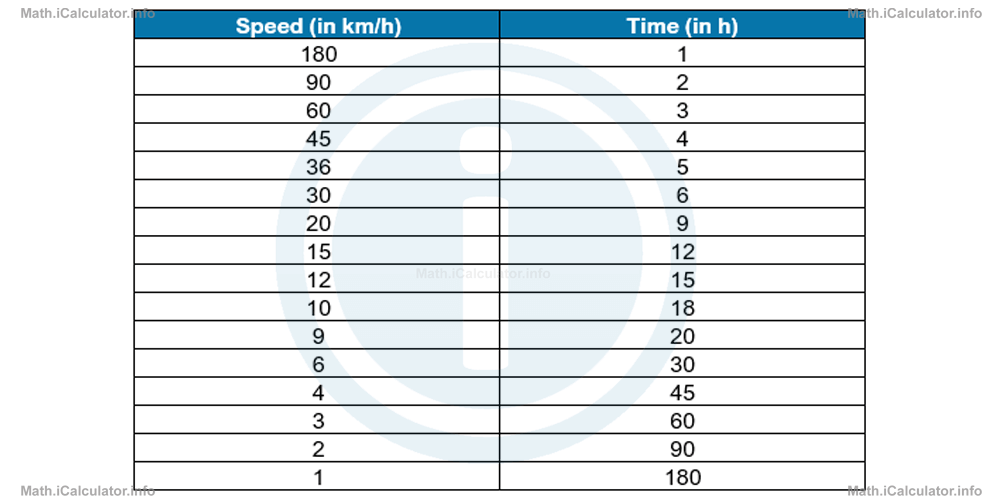
We can write the time axis in the horizontal direction as we do in Physics, while the speed values are placed in the vertical direction. The graph looks like this:
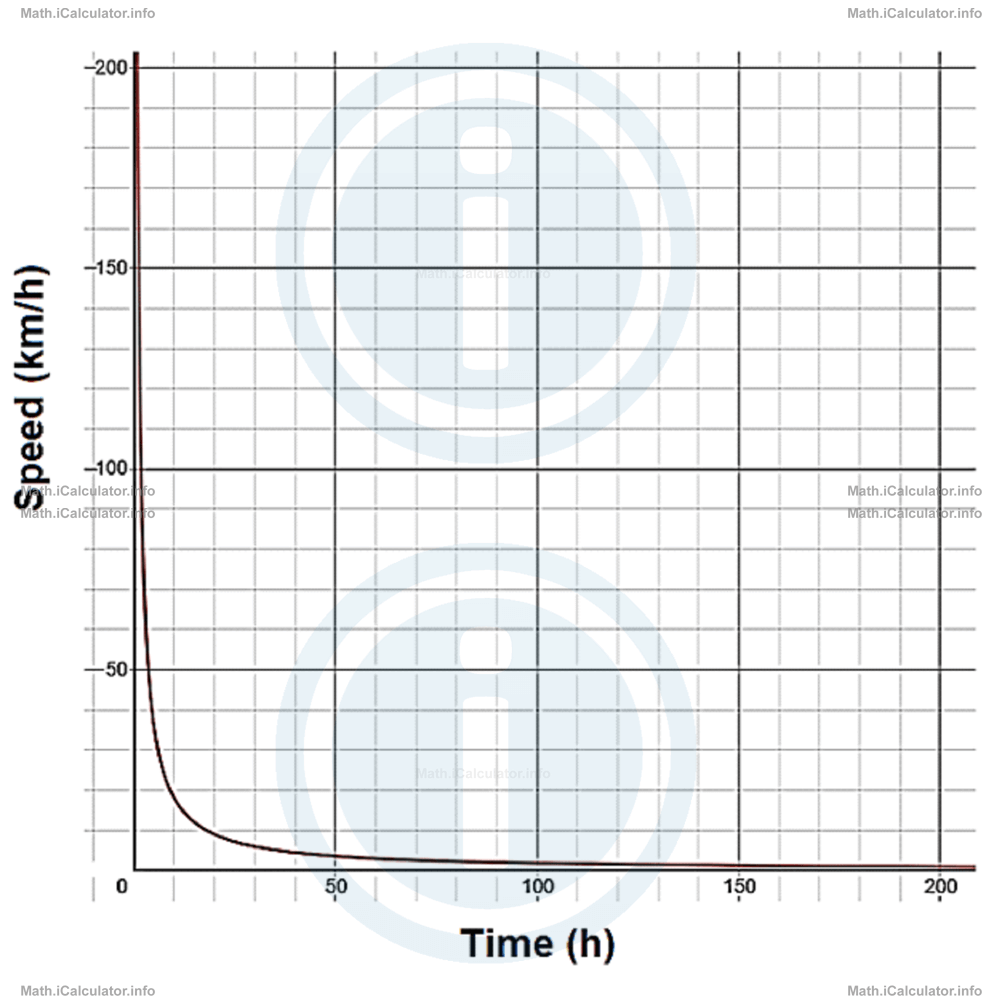
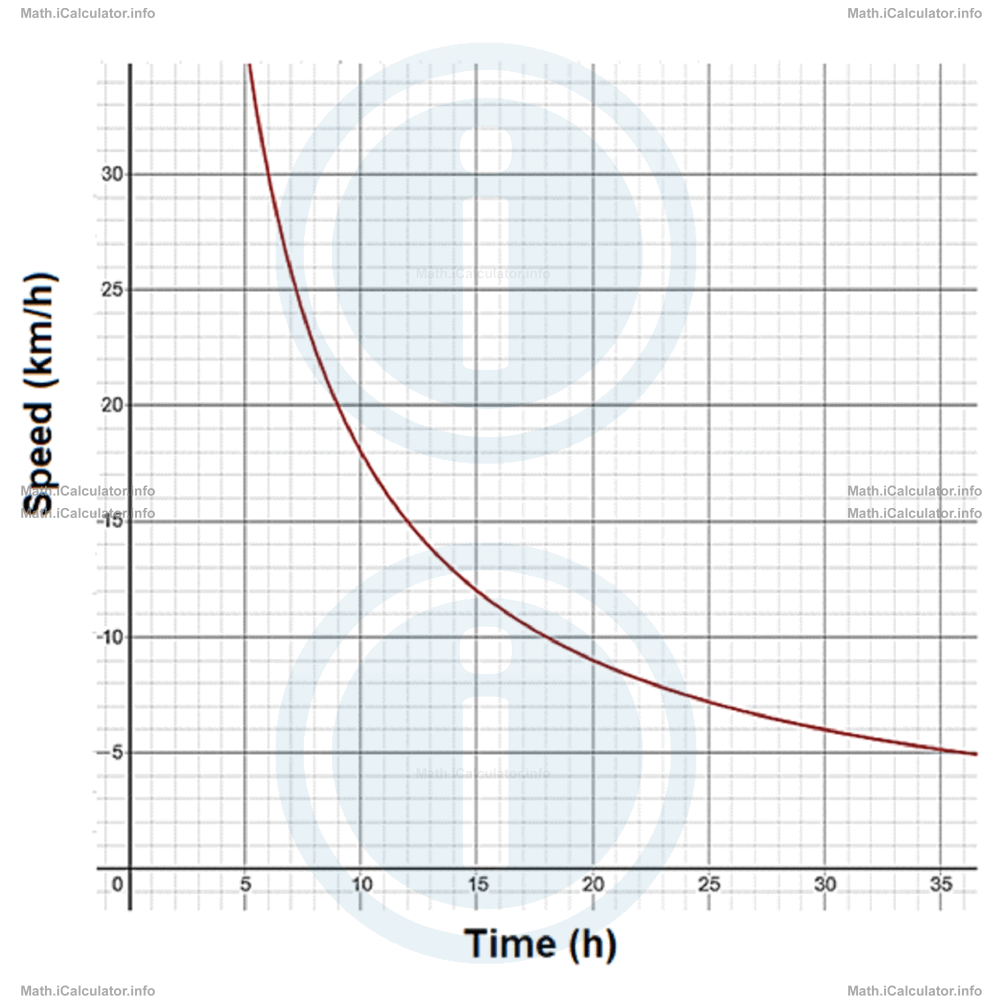
The example below provides a closer look at the graph with the part corresponding to the small values shown. This is provided to make the values of the table more evident.
Example 6
The graph of an inverse proportion is shown in the figure below.
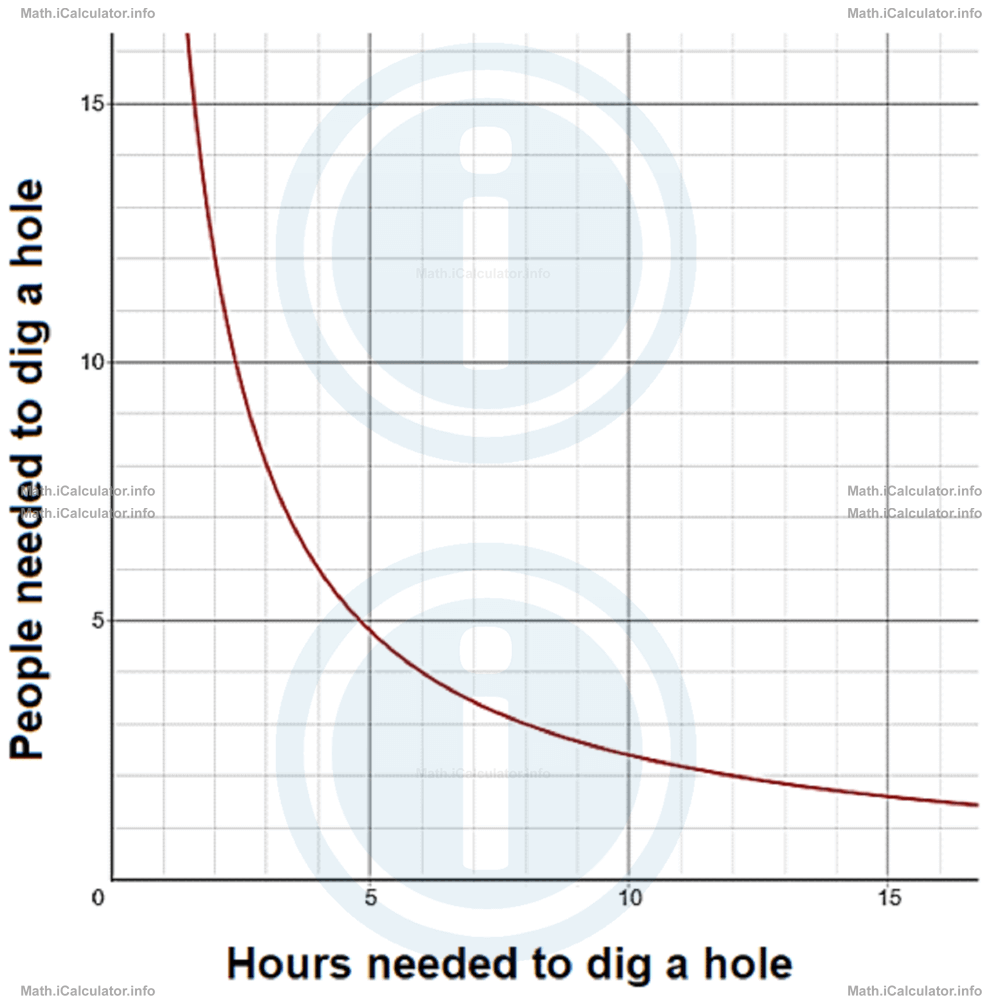
- What kind of proportionality is this?
- Calculate the constant C of this proportionality.
- How many people are needed to dig the same hole in half an hour?
- How long does it take to a single worker to dig the hole?
Solution 6
- The graph shows an inverse proportion as the graph's shape is a hyperbola.
- Since we have an inverse proportionality, the relation involved has the general form b = C/awhere b represents the number of people needed to dig the hole, a represent the number of hours needed for this work and C is the constant of proportionality.
From the graph, we see that 12 people can dig the hole in 2 hours (b = 12, a = 2). Other values that are clearly spotted in the graph include: 8 people in 3 hours (b = 8, a = 3), 6 people in 4 hours (b = 6, a = 4), etc. if we substitute one of the sets of values (for example the first from the above)in the general form of the proportion, we obtain12 = C/2Hence, the constant of proportionality C isC = 12 × 2 = 24Therefore, the inverse proportionality shown in the graph isb = 24/a - Knowing the formula of this inverse proportionality helps us find other values not indicated in the graph. Thus the number of people a needed to dig the hole in half an hour (a = 0.5) is b = 24/0.5
= 48 people - If there is a single worker available (b = 1), it takes 1 = 24/ato dig the hole.
a = 24/1
= 24 hours
More Proportion Lessons and Learning Resources
Whats next?
Enjoy the "Graph of Inverse Proportion" math lesson? People who liked the "Proportion lesson found the following resources useful:
- Inverse Graph Feedback. Helps other - Leave a rating for this inverse graph (see below)
- Ratio and Proportion Math tutorial: Proportion. Read the Proportion math tutorial and build your math knowledge of Ratio and Proportion
- Ratio and Proportion Video tutorial: Proportion. Watch or listen to the Proportion video tutorial, a useful way to help you revise when travelling to and from school/college
- Ratio and Proportion Revision Notes: Proportion. Print the notes so you can revise the key points covered in the math tutorial for Proportion
- Ratio and Proportion Practice Questions: Proportion. Test and improve your knowledge of Proportion with example questins and answers
- Check your calculations for Ratio and Proportion questions with our excellent Ratio and Proportion calculators which contain full equations and calculations clearly displayed line by line. See the Ratio and Proportion Calculators by iCalculator™ below.
- Continuing learning ratio and proportion - read our next math tutorial: Properties of Proportion. Geometric Mean
Help others Learning Math just like you
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
We hope you found this Math tutorial "Proportion" useful. If you did it would be great if you could spare the time to rate this math tutorial (simply click on the number of stars that match your assessment of this math learning aide) and/or share on social media, this helps us identify popular tutorials and calculators and expand our free learning resources to support our users around the world have free access to expand their knowledge of math and other disciplines.
Ratio and Proportion Calculators by iCalculator™
- Geometric Mean Calculator
- Joint Variation Calculator
- Ratio Calculator
- Ratio Solver
- Ratio Addition Calculator
- Ratio Subtraction Calculator
- Ratio Division Calculator
- Ratio Multiplication Calculator
- Relative Ratios Calculator
- Ratio Comparison Calculator
- Visual Ratio Calculator
- Ratio Finder
- Equivalent Ratios Calculator
- Equivalent Ratio Table Calculator
- Aspect Ratio Calculator
- Divide Ratio Calculator
- Ratio Divider Calculator
- Ratio Simplifier Calculator
- Golden Ratio Calculator
- 3 Ratio Calculator
- Sharing Ratio Calculator
- Equal Share Verse Ratio Share Calculator
- Values To Ratio Calculator
- Ratio Table Calculator
- Ratio Table
- Decimal Ratio Table Calculator
- Ratio Table Creator
- Ratio Converter
- Percentage To Ratio Calculator
- Ratio To Percentage Calculator
- Ratio To Fraction Calculator
- Fraction To Ratio Calculator
- Ratio To Decimal Calculator
- Decimal To Ratio Calculator
- Values To Ratio Calculator
- Which Ratio Or Fraction Is Bigger
- Which Ratio Or Percentage Is Bigger
- Which Ratio Is Bigger