Menu
Quadratic Inequalities - Revision Notes
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
In addition to the revision notes for Quadratic Inequalities on this page, you can also access the following Inequalities learning resources for Quadratic Inequalities
| Tutorial ID | Title | Tutorial | Video Tutorial | Revision Notes | Revision Questions | |
|---|---|---|---|---|---|---|
| 10.2 | Quadratic Inequalities |
In these revision notes for Quadratic Inequalities, we cover the following key points:
- What are quadratic inequalities?
- How to identify whether a given number is a root of a quadratic inequality or not?
- How to write a quadratic inequality in the standard form?
- What happens to the sign of a quadratic inequality when the discriminant is positive? Zero? Negative?
- How to study the sign of a quadratic inequality?
- How to find the solution set(s) of a quadratic inequality?
Quadratic Inequalities Revision Notes
Linear inequalities have a similar structure with linear equalities except for the sign, which must be one of the four known inequality signs. The four possible general forms of quadratic inequalities are:
ax2 + bx + c < 0
ax2 + bx + c ≥ 0
ax2 + bx + c ≤ 0
If a quadratic inequality is not in one of the four standard forms written above, we must turn it into the standard form, where the most appropriate thing would be to have the coefficient a positive.
Solving a quadratic inequality means finding the set of values of the variable, which makes the inequality true. Obviously, it is not possible to find the solution set of a quadratic inequality simply by guessing or trying all values that come to mind. Therefore, we must find a general method for definitely solving such inequalities. This method consists of studying the inequality sign. For this, we also have to take into account the corresponding quadratic equation, which helps to determine the boundary values where the sign of the inequality changes.
There are three cases to consider when solving a quadratic equation by studying the sign:
- The discriminant of the corresponding quadratic equation is positive
The first rule we use to solve a linear inequality by studying the sign is as follows:
"If the discriminant of the corresponding quadratic equation is positive, the quadratic inequality has the opposite sign of the constant a between the roots and the sign of the coefficient a aside from the interval between the two roots."
This rule is illustrated in the scheme below.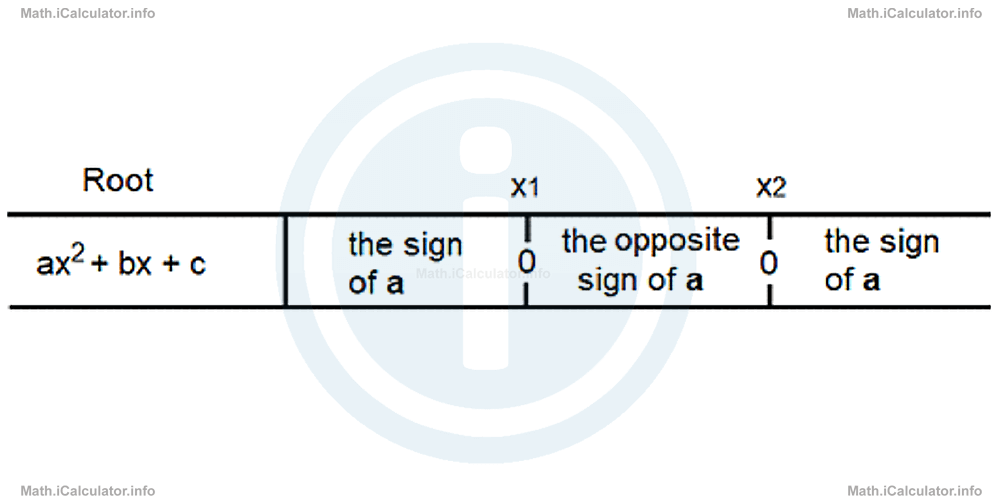
- The discriminant of the corresponding quadratic equation is zero
In this case, the interval between the two roots in the previous case narrows and becomes zero, as the two roots converge. Therefore, we have only one zero point, where the quadratic inequality turns into a quadratic equation, while for the rest of the values the quadratic expression has the sign of the coefficient a, as shown in the scheme below.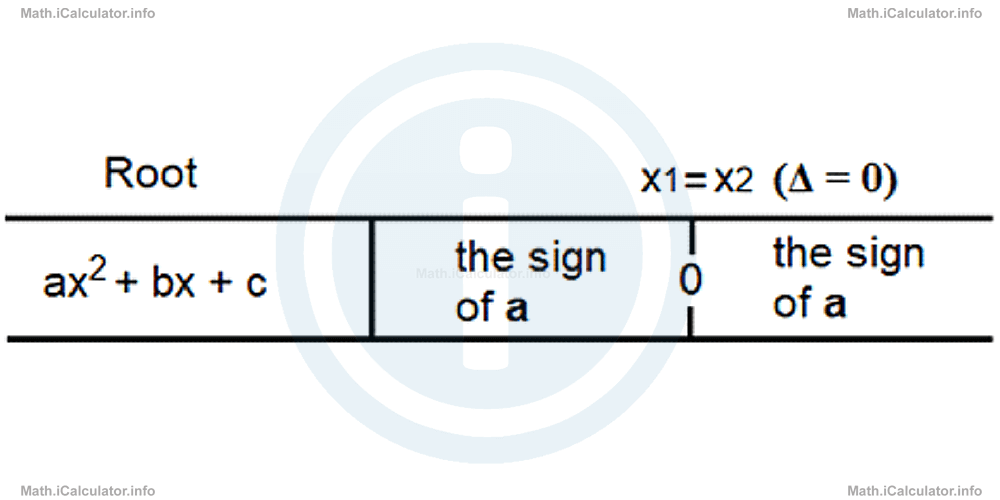
- The discriminant of the corresponding quadratic equation is negative
In this case, the bordering value that separates the two intervals where the zone taking the sign of the coefficient a does not exist anymore, as the corresponding quadratic equation cannot have any solution as in the previous two cases. There were precisely such solution points that made possible the separation between the zones. Therefore, the quadratic inequalities have everywhere the sign of the coefficient a, as shown in the scheme below.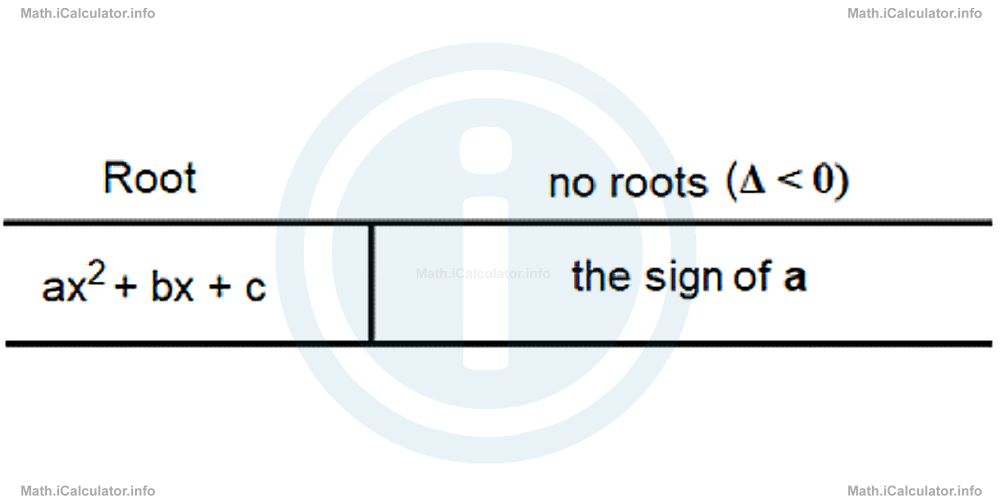
Whats next?
Enjoy the "Quadratic Inequalities" revision notes? People who liked the "Quadratic Inequalities" revision notes found the following resources useful:
- Revision Notes Feedback. Helps other - Leave a rating for this revision notes (see below)
- Inequalities Math tutorial: Quadratic Inequalities. Read the Quadratic Inequalities math tutorial and build your math knowledge of Inequalities
- Inequalities Video tutorial: Quadratic Inequalities. Watch or listen to the Quadratic Inequalities video tutorial, a useful way to help you revise when travelling to and from school/college
- Inequalities Practice Questions: Quadratic Inequalities. Test and improve your knowledge of Quadratic Inequalities with example questins and answers
- Check your calculations for Inequalities questions with our excellent Inequalities calculators which contain full equations and calculations clearly displayed line by line. See the Inequalities Calculators by iCalculator™ below.
- Continuing learning inequalities - read our next math tutorial: Graphing Inequalities
Help others Learning Math just like you
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
We hope you found this Math tutorial "Quadratic Inequalities" useful. If you did it would be great if you could spare the time to rate this math tutorial (simply click on the number of stars that match your assessment of this math learning aide) and/or share on social media, this helps us identify popular tutorials and calculators and expand our free learning resources to support our users around the world have free access to expand their knowledge of math and other disciplines.