Menu
Math Lesson 10.4.3 - Systems of Three Linear Inequalities
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
Welcome to our Math lesson on Systems of Three Linear Inequalities, this is the third lesson of our suite of math lessons covering the topic of Systems of Inequalities, you can find links to the other lessons within this tutorial and access additional Math learning resources below this lesson.
Solving Systems of Three Linear Inequalities
Sometimes, a third inequality is added to the normal systems of two linear inequalities, producing a system of three linear inequalities. The simplest case is when the third inequality contains a single variable and acts as a third boundary line for the solution zone. In this way, we often obtain a closed figure (triangle) as a solution zone, formed by the two-by-two intercepts of the three lines, as shown in the example below.
Example 3
- Identify the solution zone of the system of linear inequalities 3x + 2y < 1-2x + 5y > -2x ≥ -2
- Check whether points A(-3, 2), B(-1, 1) and C(2, 0) belong to the solution zone of this system.
- Find the coordinates of graphs intercepts.
Solution 3
- First, we have to turn all inequalities in the form y (?) mx + n to identify the individual solution zones. Thus, for the first inequality, we have 3x + 2y < 1This means the solution zone of the above inequality lies under its graph line.
2y < -3x + 1
2y/2 < -3x/2 + 1/2
y < -3x/2 + 1/2
For the second inequality, we have-2x + 5y > -2This means the solution zone of the above inequality lies above its graph line.
5y > 2x - 2
5y/5 > 2x/5 - 2/5
y > 2x/5 - 2/5
As for the third inequality, it is not necessary to do any operation as it is clear that the solution zone lies on the right of the vertical line x = 2, including the line itself. Therefore, based on the above findings we obtain the following figure: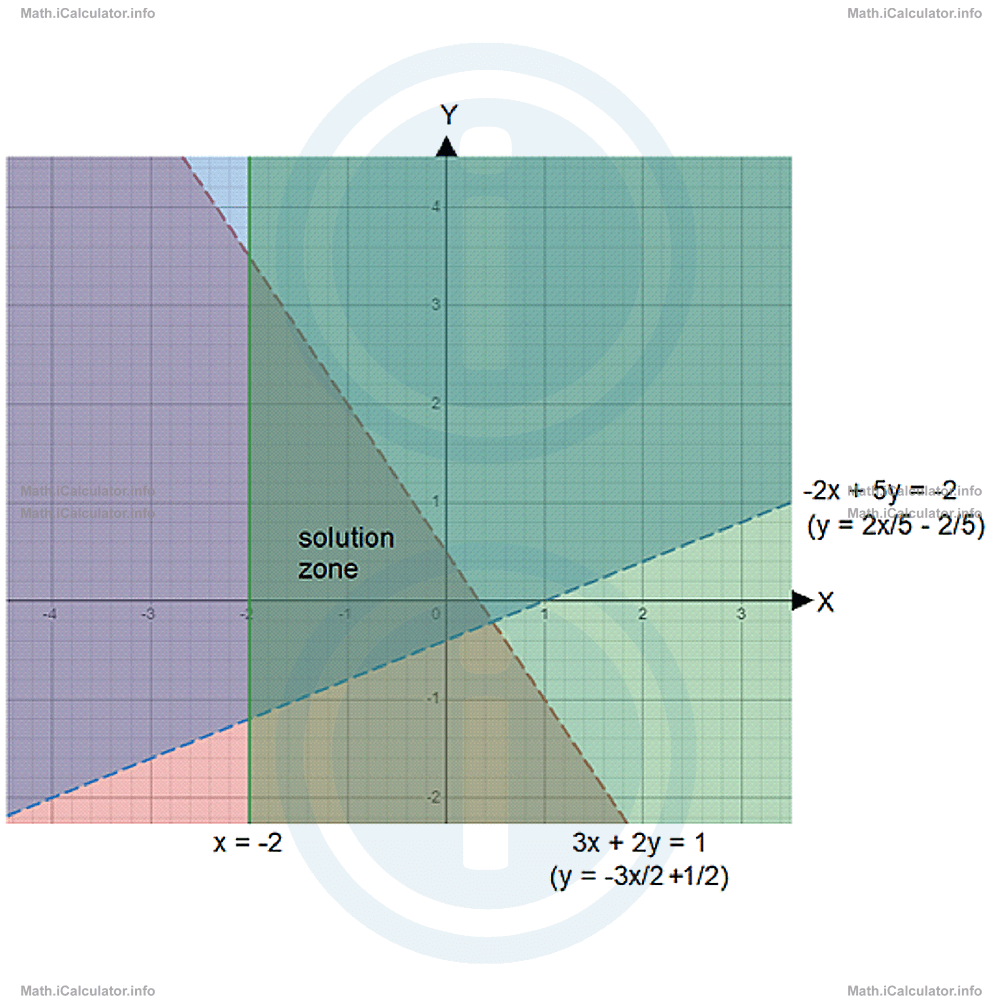
- Now, we have to check whether points A(-3, 2), B(-1, 1) and C(2, 0) belong to the solution zone of this system by substituting each point in the inequalities of the system and see whether this substitution gives true inequalities or not. Thus, for point A(x = -3 and y = 2), we have 3x + 2y < 1-2x + 5y > -2x ≥ -2Since not all inequalities are true for the coordinates of point A, this point does not belong to the solution set of this system of inequalities.
3 ∙ (-3) + 2 ∙ 2 < 1-2 ∙ (-3) + 5 ∙ 2 > -2-3 ≥ -2
-9 + 4 < 1-6 + 10 > -2-3 ≥ -2
-5 < 1 (true)4 > -2 (true)-3 ≥ -2 (false)
For point B(-1, 1) where x = -1 and y = 1, we obtain3x + 2y < 1-2x + 5y > -2x ≥ -2Since all inequalities are true for the coordinates of point B, this point belongs to the solution set of this system of inequalities.
3 ∙ (-1) + 2 ∙ 1 < 1-2 ∙ (-1) + 5 ∙ 1 > -2-1 ≥ -2
-3 + 2 < 12 + 5 > -2-1 ≥ -2
-1 < 1 (true)7 > -2 (true)-1 ≥ -2 (true)
Last, let's check whether point C(2, 0) where x = 2 and y = 0 belongs to the solution zone of the given system of linear inequalities or not. We have3x + 2y < 1-2x + 5y > -2x ≥ -2Since not all inequalities are true for the coordinates of point C, this point does not belong to the solution set of this system of inequalities.
3 ∙ 2 + 2 ∙ 0 < 1-2 ∙ 2 + 5 ∙ 0 > -22 ≥ -2
6 + 0 < 1-4 + 0 > -22 ≥ -2
6 < 1 (false)-4 > -2 (false)2 ≥ -2 (true) - To find the intercepts, i.e. the points that form the vertices of the triangle which includes the solution zone, we consider two by two the corresponding equations obtained by the three given inequalities. Thus, for the first vertex, we obtain the following system of linear equations 3x + 2y = 1-2x + 5y = -2Let's eliminate the variable x by multiplying the first inequality by 2 and the second one by 3 and eventually add the two equations. Thus,2 ∙ (3x + 2y) = 2 ∙ 13 ∙ (-2x + 5y) = 3 ∙ (-2)We find the x-coordinate of the first vertex by substituting the above y-coordinate in any of the equations in the system; for example in the first. Thus,
6x + 4y = 2-6x + 15y = -6
-19y = -4
y = -4/193x + 2 ∙ (-4)/19 = 1Therefore, one of the intercepts (the bottom left) has the coordinates (9/19, -4/19).
3x - 8/19 = 1
3x = 1 + 8/19
3x = 19/19 + 8/19
3x = 27/19
x = 27 ÷ 3/19
= 9/19
Now, let's find the second intercept by solving the system3x + 2y = 1x = -2This system is solved easier by substituting x = -2 in the first equation. This yield,3 ∙ (-2) + 2y = 1Therefore, the second intercept (the top-left one) is at (-2, 7/2).
-6 + 2y = 1
2y = 1 - (-6)
2y = 7
y = 7/2
Last, we find the third intercept by solving the linear system-2x + 5y = -2x = -2Again, we solve this system by substituting x = -2 in the first equation. Thus,-2 ∙ (-2) + 5y = -2Therefore, the third graphs' intercept (the bottom-left one) has the coordinates (-2, -6/5).
4 + 5y = -2
5y = -2 - 4
5y = -6
y = -6/5
It is not always possible to obtain a closed region (like the triangle in the above example) as a solution zone for a system of three linear inequalities. For example, if two of the linear inequalities are dependent (i.e. when they have parallel graphs), we obtain a zone that is limited in two or three directions but unlimited in the fourth, as the graphs form a figure where two parallel lines are intercepted by a third one. Let's consider an example to clarify this point.
Example 4
Solve graphically the system of linear inequalities
- x - 2y < 13x - 6y ≤ 5x < 2
- Find the coordinates of the highest point of the solution set.
Solution 4
- We have two write the first inequalities in the form y (?) mx + n. Thus, for the first inequality, we have x - 2y < 1Hence, the solution set of this inequality alone consists of the region above the graph.
-2y < 1 - x
-2y/-2 < 1 - x/-2
y > -1/2 + -x/-2
y > x/2 - 1/2
For the second inequality, we have3x - 6y ≤ 5Hence, the solution set of this inequality alone consists of the region above the graph including the graph line.
-6y ≤ -3x + 5
-6y - 6 ≤ -3x/-6 + 5/-6
y ≥ x/2 - 5/6
The third inequality includes the region on the left of the graph without including the vertical line x = 2/.
Hence, the graphical solution to this system of inequalities is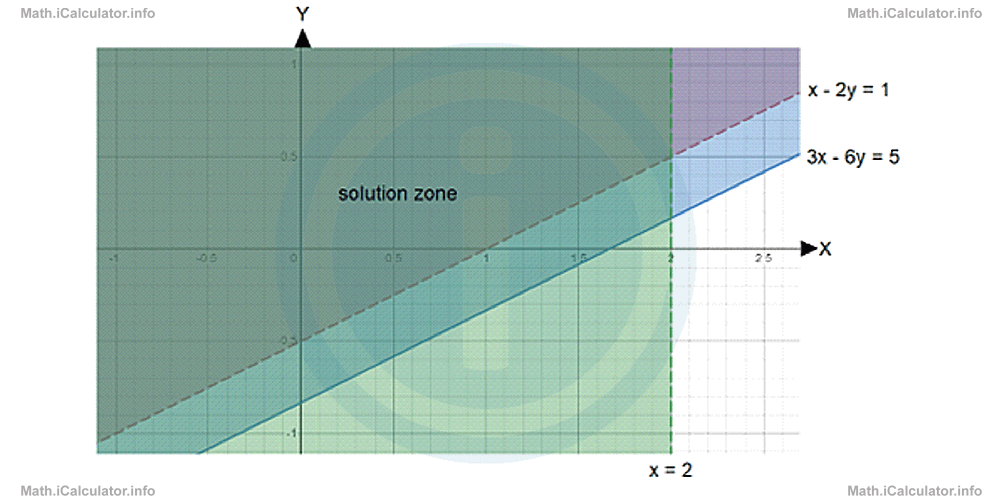
More Systems of Inequalities Lessons and Learning Resources
Whats next?
Enjoy the "Systems of Three Linear Inequalities" math lesson? People who liked the "Systems of Inequalities lesson found the following resources useful:
- Three Linear Feedback. Helps other - Leave a rating for this three linear (see below)
- Inequalities Math tutorial: Systems of Inequalities. Read the Systems of Inequalities math tutorial and build your math knowledge of Inequalities
- Inequalities Video tutorial: Systems of Inequalities. Watch or listen to the Systems of Inequalities video tutorial, a useful way to help you revise when travelling to and from school/college
- Inequalities Revision Notes: Systems of Inequalities. Print the notes so you can revise the key points covered in the math tutorial for Systems of Inequalities
- Inequalities Practice Questions: Systems of Inequalities. Test and improve your knowledge of Systems of Inequalities with example questins and answers
- Check your calculations for Inequalities questions with our excellent Inequalities calculators which contain full equations and calculations clearly displayed line by line. See the Inequalities Calculators by iCalculator™ below.
- Continuing learning inequalities - read our next math tutorial: Solving Linear Inequalities
Help others Learning Math just like you
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
We hope you found this Math tutorial "Systems of Inequalities" useful. If you did it would be great if you could spare the time to rate this math tutorial (simply click on the number of stars that match your assessment of this math learning aide) and/or share on social media, this helps us identify popular tutorials and calculators and expand our free learning resources to support our users around the world have free access to expand their knowledge of math and other disciplines.