The Definition of Monomials and Polynomials - Revision Notes

In these revision notes for The Definition of Monomials and Polynomials, we cover the following key points:

• What are monomials? What is their structure?
• What are the components of a monomial?
• What is a polynomial?
• What is the difference between a polynomial and an algebraic expression?
• What does a term of a polynomial represent?
• What is the difference between coefficients and constants in a polynomial?
• What is the degree of a polynomial? How do we find it?
• How do we name polynomials based on their degree?
• How do we find the value of polynomials?
• What are the zeroes of a polynomial? How would you find them?
• How do you find the zeroes of high-order polynomials?
• What are homogenous and non-homogenous polynomials? How do you know which of these categories a polynomial does belong?

The Definition of Monomials and Polynomials Revision Notes

A monomial is an algebraic expression consisting of the product of a real number called a coefficient and one or more letters representing variables, which are raised to certain natural powers.

Polynomials are algebraic expressions that contain two or more monomials that are added to or subtracted from each other. "Poly" means "many" in Greek. Hence, the term "polynomial" is translated as "many monomials put together". Monomials, therefore, represent a special case of polynomials; we can call them polynomials with one term.

If we have a number not followed by a variable in a polynomial, it still represents a term, but the number itself is not called a coefficient anymore but a constant instead.

Polynomials are special algebraic expressions where all exponents of the variables are in whole powers (natural plus zero). In other words, polynomials belong to the algebraic expression set, but they do not represent the entire set of the algebraic expressions.

We express the general form of a polynomial as P(x, y, z, ) where z, y, z, etc., are its variables.

The degree of a polynomial is the greatest of the sum of variables' indices for every single monomial. In other words, to determine the degree of a polynomial, the indices of different variables contained in a single monomial are added to each other. This procedure is carried out for all monomials separately. Then, we compare the sums obtained to determine the degree of the given polynomial.

Polynomials are assigned names according to the degree they hold. They are shown in the table below.

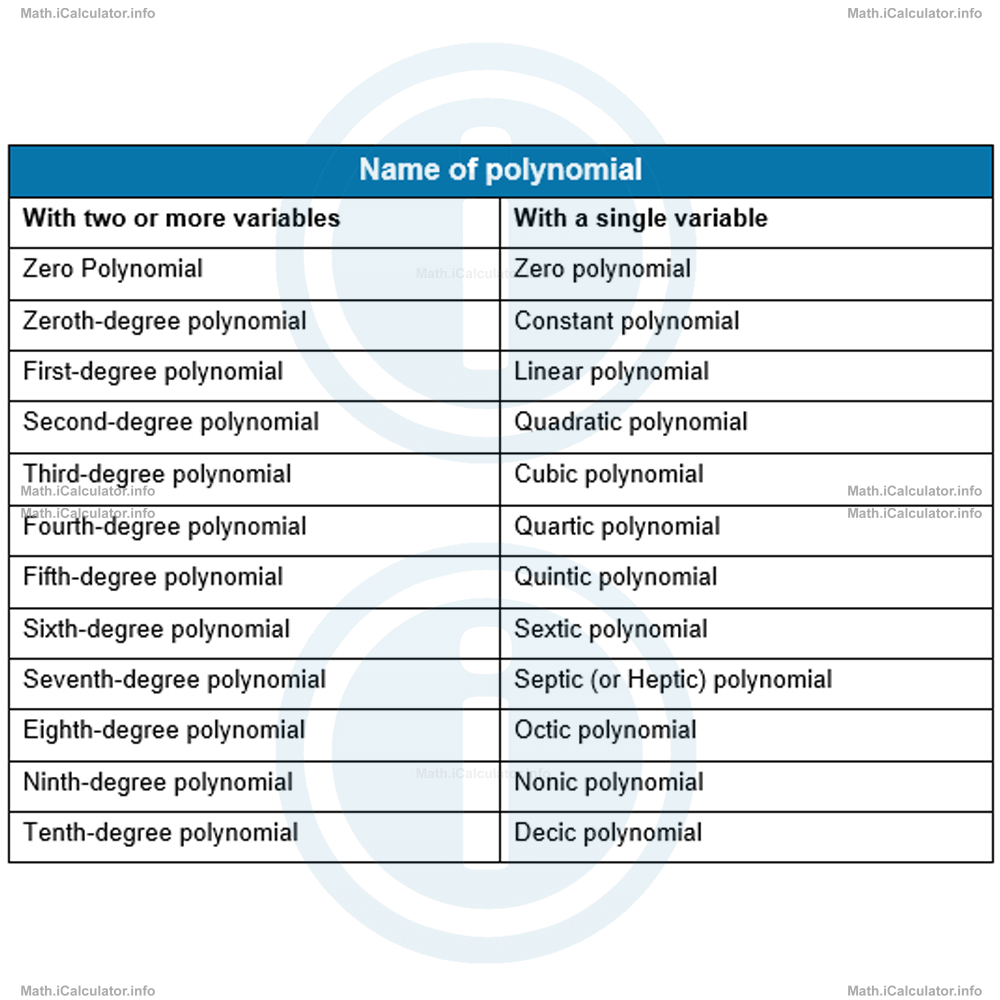
We can find the value of polynomials by substituting the variables with numbers. The same procedure is used for polynomials with two or more variables as well.

Sometimes, it is very useful to know the values of the variables of a polynomial for which the polynomial becomes zero. These values are known as the zeroes of the polynomial. For example, when factoring, simplifying or dividing two polynomials, it is useful to know the zeroes, as the abovementioned operations are done easier.

Constant polynomials do not have zeroes, as such polynomials contain only numbers, so it is impossible to make them zero. On the other hand, linear polynomials have one zero at maximum. The zeroes of a quadratic polynomial represent the roots of the corresponding quadratic equation.

We can find the zeroes of higher-order polynomials by applying any of the known iterative methods. We can use intuition to identify two values of the variable that give numbers with opposite signs as results. Since the given zero of the polynomial lies in that interval, we can narrow it until you obtain the zero of the polynomial to the desired precision.

Knowing the degree of a polynomial, therefore, is very important, as it gives the maximum possible zeroes it may have. In other words, a nth degree polynomial may have n or less zero points. This means the corresponding equation when P(x) is taken as 0, has n roots at maximum.

When a multivariable polynomial has the same degree in all its terms, it is called homogenous. Hence, knowing the degree of a polynomial has another advantage, as this helps in finding whether the given polynomial expression is homogeneous or not.