Solutions for Polynomial Equations - Revision Notes

In these revision notes for Solutions for Polynomial Equations, we cover the following key points:

• What is the synthetic division method of polynomials?
• What are the components of the division of two polynomials?
• What is the procedure used in the division of polynomials when using the Synthetic Division Method?
• What are the roots of a polynomial? How to find them?
• What does the Rational Root (Zero) Theorem say?
• Why the Rational Root (Zero) Theorem is useful in solving polynomial equations?
• How to list all possible roots (zeroes) of a polynomial equation?
• How to identify the zeroes of a polynomial from the whole list of possible zeroes?
• How to solve polynomial equations?

Solutions for Polynomial Equations Revision Notes

The synthetic division method is a method used to divide polynomials in a much simpler way compared to the long division method. The condition to perform a synthetic division is to have a linear polynomial as a divisor, i.e. the divisor Q(x) of the polynomial P(x) must have the form mx ± n, where m is a coefficient and n a constant.

We can write the division of two polynomials P(x) and Q(x) as

where S(x) is the quotient polynomial and R(x) is the remainder polynomial.

The Synthetic Division Method of Polynomials is represented schematically through the figure below:

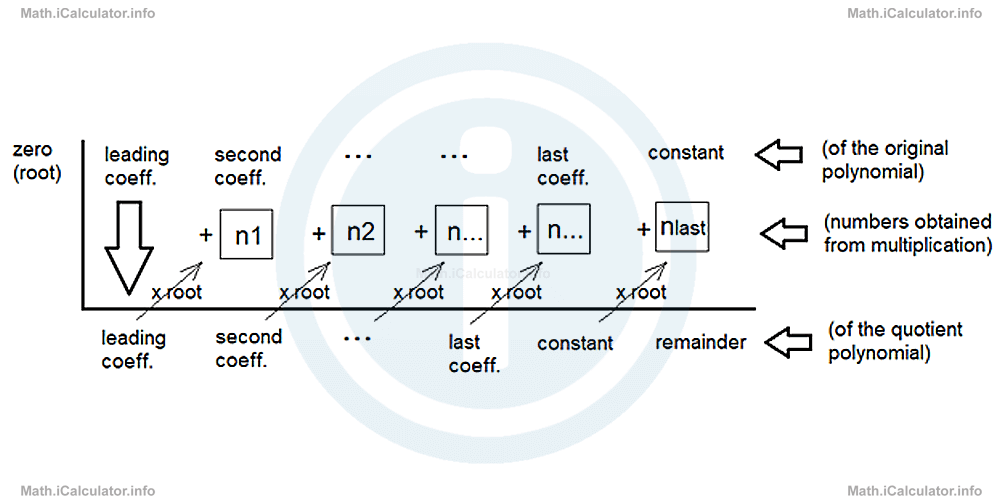
The procedure to perform the synthetic division of polynomials is as follows:

Step 1: Write down the coefficients and the constant of the original polynomial P(x) at the place where we write the dividend when using the long division method. In addition, we write the zero of the divisor Q(x) in the place where we put the divisor in the long division method.

Step 2: Bring the leading coefficient of the original polynomial to the bottom row.

Step 3: Multiply the leading coefficient of the polynomial with the zero of the divisor and write down the result in the middle row below the second coefficient.

Step 4: Add the numbers in the second column and write down the result in the bottom row, next to the leading coefficient.

Step 5: Repeat the procedure explained in step 3 but this time using the new number.

Step 6: Repeat the procedure explained in step 4 but this time using the new number.

Step 7: Since there are no more operations to do, the last number obtained gives the remainder of the division. On the other hand, the number preceding it represents the constant of the quotient and the number preceding it, the last coefficient of the quotient polynomial and so on.

The Rational Zero Theorem (otherwise known as the Rational Root Theorem), as its name suggests, is used to find rational solutions when dealing with a polynomial equation (or zeros or roots of a polynomial expression).

Not always, a polynomial has zeroes. This means that not always the corresponding polynomial equations must have zeroes. But when they have, these zeroes must be rational numbers. Given that the general form of a polynomial is

or

It is known that all values of the variable x for which P(x) = 0 are the zeroes (roots) of the polynomial.

The Rational Root Theorem states that all rational roots of a polynomial equation with integer coefficients have the form p/q, where p is a factor of the polynomial constant a₀ and q is a factor of the leading coefficient a_n. The two numbers p and q must be relatively prime.

The Rational Root Theorem helps identify the possible roots of a polynomial equation. This means it helps narrow the range of possible rational roots but it doesn't give the exact roots of a polynomial equation. If exist, they are found by applying the extra procedure explained below.

Step 1: Identify the constant of the polynomial and write down all its integer factors, including the negative ones. This helps identify the possible values of p.

Step 2: Identify the leading coefficient an of the polynomial and write down its integer factors q.

Step 3: Find all possible values of p/q.

Step 4: Remove all duplicates resulting from step 3.

Not all values listed through the above procedure are roots of a given polynomial. A polynomial may have a maximum number of roots that correspond to its degree. Hence, we have to reject most of the possible roots identified when using the above method.

There are two possible ways to identify all rational zeroes of the polynomial P(x):

1. Substituting all possible zeroes found earlier in the polynomial P(x) and check for which of these values we have P(x) = 0.
2. Using the Synthetic Division Method for each possible zero and see which of them give no remainder.

One can prove the correctness of the results obtained by using the Synthetic Division Method of Polynomials.

Another advantage of the method described above is that after having identified all zeroes of the polynomial, we can write all possible forms of factorisation for the given polynomial. The coefficients and the constant of the quotient polynomials appear in the last row. At this point, it is worth to state that the degree of the quotient polynomial is one less than that of the original polynomial.

Finding all rational roots of a polynomial P(x) means solving the corresponding polynomial equation P(x) = 0. Hence, the procedure described above is also used to solve polynomial equations of whatever degree. The only restriction is that all coefficients and the constant of the given polynomial must be integers. Otherwise, the polynomial equation must be solved using the computerized methods.

In short, all polynomial equations are solved by combining the Rational Root Theorem and the Synthetic Division Method, as explained in this tutorial.