Menu
Working with Arithmetic and Geometric Series. How to find the Sum of the First n-Terms of a Series.
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
The following math revision questions are provided in support of the math tutorial on Working with Arithmetic and Geometric Series. How to find the Sum of the First n-Terms of a Series.. In addition to this tutorial, we also provide revision notes, a video tutorial, revision questions on this page (which allow you to check your understanding of the topic) and calculators which provide full, step by step calculations for each of the formula in the Working with Arithmetic and Geometric Series. How to find the Sum of the First n-Terms of a Series. tutorials. The Working with Arithmetic and Geometric Series. How to find the Sum of the First n-Terms of a Series. calculators are particularly useful for ensuring your step-by-step calculations are correct as well as ensuring your final result is accurate.
Not sure on some or part of the Working with Arithmetic and Geometric Series. How to find the Sum of the First n-Terms of a Series. questions? Review the tutorials and learning material for Working with Arithmetic and Geometric Series. How to find the Sum of the First n-Terms of a Series.
Working with Arithmetic and Geometric Series. How to find the Sum of the First n-Terms of a Series. Revision Questions
1. . What is S7 in the number series 3, 5, 8, 12, …?
- 28
- 30
- 68
- 98
Correct Answer: D
2. . What is the sum of the first 20 terms in the number series 6, 9, 12, 15, …?
- 690
- 670
- 63
- 42
Correct Answer: A
3. . The first term of an arithmetic series is 8 and the sum of the first five terms in this series is 100. What is the common difference d between the consecutive terms?
- 4
- 6
- 8
- 10
Correct Answer: B
4. . What is the number of terms in the series 3 + 11 + 19 + … + 131?
- 123
- 17
- 16
- 15
Correct Answer: B
5. . What is 2 + 9 + 16 + 23 + … + 72 + 79?
- 486
- 567
- 972
- 1134
Correct Answer: A
6. . The first term of an arithmetic progression is 9 and the sixth term is 29. What is the sum of the first six terms of this sequence?
- 38
- 85
- 114
- 200
Correct Answer: C
7. . The third term of an arithmetic sequence is 32 and the seventh term of the same sequence is 4. What is the sum of the first 13 terms of this sequence?
- 56
- 52
- 48
- 44
Correct Answer: B
8. . What is the sum of the first 10 terms of the arithmetic series 13 + 4 + (-5) + …?
- 8
- 275
- -275
- 0
Correct Answer: C
9. . What is the sum of the first 5 terms of the geometric sequence with general term
- 50,625
- 2343
- 2340
- 1875
Correct Answer: B
10. . What is 3 + 6 + 9 + … + 186 + 189?
- 2048
- 4096
- 6048
- 6144
Correct Answer: C
11. . Find the sum of the first 32 terms of the following series
- 752
- -800
- 1552
- -48
Correct Answer: D
12. . The second term of a geometric sequence is 10 and the fifth term of the same sequence is 1250. What is the sum of the first 6 terms of the corresponding geometric series?
- 7,812
- 15,624
- 15,625
- 39,060
Correct Answer: B
13. . The first term of a geometric progression is 243 and the fourth term is 9. Find the common ratio.
- 9
- -9
- 3
- -3
Correct Answer: D
14. . What is the sum of the first 10 terms of the series 4 + 12 + 36 + …?
- 59,048
- 59,049
- 118,096
- 118,098
Correct Answer: C
15. . What is the sum of the first 10 terms of the number series 64 + 32 + 16 + …?
- 15
- 1023/8
- 1023
- 1024
Correct Answer: B
16. . The sum of the first n terms, Sn of a particular arithmetic progression is given by Sn = 7n - 3n2. What is the first term of this progression?
- 1
- 3
- 7
- 14
Correct Answer: D
17. . The sum of the first n terms, Sn of a particular arithmetic progression is given by Sn = 2n + 9n2. What is the fourth term of this progression?
- 72
- 36
- 18
- 9
Correct Answer: A
18. . A customer wants to buy a new house for $130,000 but he has only $30,000 in his savings account. Therefore, the customer agrees to make the rest of payment in 40 installments according to an arithmetic progression formula, where the first payment is $1000 with a total interest of 10%. Calculate the amount of the last installment.
- $3500
- $4500
- $5500
- $6500
Correct Answer: B
19. . The monthly salary of a football player increases by 20% for every goal he scores in an official match. The base salary of this player is $60,000/month. How much did he earn in total in the first three months in which he scored 2, 3 and 4 goals respectively in all official matches?
- $324,496
- $124,416
- $103,680
- $86,400
Correct Answer: A
20. . The upper part of a wall is shown in the figure below.
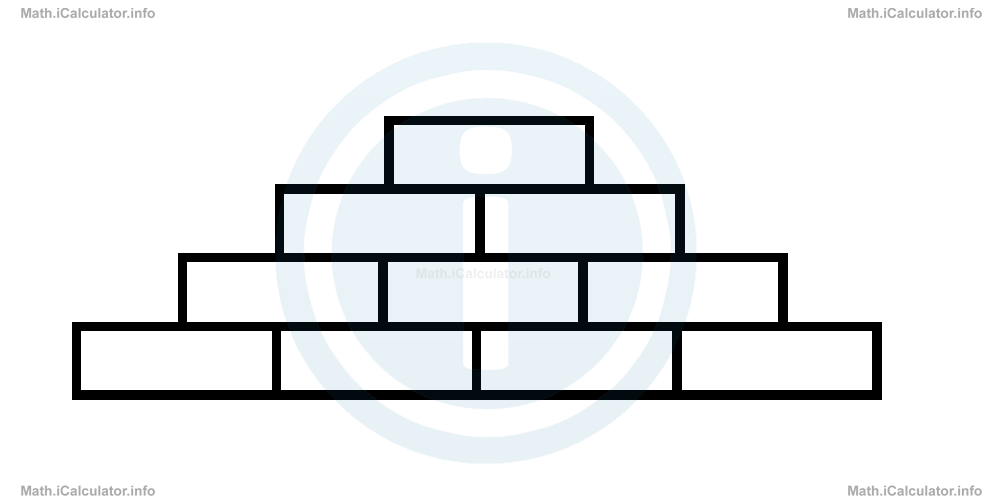
How many bricks does this wall have in total if it has 12 rows?
- 30
- 48
- 72
- 144
Correct Answer: C
Whats next?
Enjoy the "Working with Arithmetic and Geometric Series. How to find the Sum of the First n-Terms of a Series." practice questions? People who liked the "Working with Arithmetic and Geometric Series. How to find the Sum of the First n-Terms of a Series." practice questions found the following resources useful:
- Practice Questions Feedback. Helps other - Leave a rating for this practice questions (see below)
- Sequences and Series Math tutorial: Working with Arithmetic and Geometric Series. How to find the Sum of the First n-Terms of a Series.. Read the Working with Arithmetic and Geometric Series. How to find the Sum of the First n-Terms of a Series. math tutorial and build your math knowledge of Sequences and Series
- Sequences and Series Video tutorial: Working with Arithmetic and Geometric Series. How to find the Sum of the First n-Terms of a Series.. Watch or listen to the Working with Arithmetic and Geometric Series. How to find the Sum of the First n-Terms of a Series. video tutorial, a useful way to help you revise when travelling to and from school/college
- Sequences and Series Revision Notes: Working with Arithmetic and Geometric Series. How to find the Sum of the First n-Terms of a Series.. Print the notes so you can revise the key points covered in the math tutorial for Working with Arithmetic and Geometric Series. How to find the Sum of the First n-Terms of a Series.
- Check your calculations for Sequences and Series questions with our excellent Sequences and Series calculators which contain full equations and calculations clearly displayed line by line. See the Sequences and Series Calculators by iCalculator™ below.
- Continuing learning sequences and series - read our next math tutorial: Binomial Expansion and Coefficients
Help others Learning Math just like you
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
We hope you found this Math tutorial "Working with Arithmetic and Geometric Series. How to find the Sum of the First n-Terms of a Series." useful. If you did it would be great if you could spare the time to rate this math tutorial (simply click on the number of stars that match your assessment of this math learning aide) and/or share on social media, this helps us identify popular tutorials and calculators and expand our free learning resources to support our users around the world have free access to expand their knowledge of math and other disciplines.