Math Revision 17.1 - Sets Definition and Notation. Representing Sets

In these revision notes for Sets Definition and Notation. Representing Sets, we cover the following key points:

• What are sets? How to express them?
• What are the number sets available?
• What are the elements of a set? How to express them?
• What are finite and infinite sets?
• What is the empty set? Why is it important?
• What are subsets? How to express them?
• How to find the number of subsets in a given set?
• What is the power set?
• What is the universal set? How to find it?
• What are the methods of representing sets?
• When two sets are equivalent? Equal? Different?

Sets Definition and Notation. Representing Sets Revision Notes

By definition, a set is a collection of items that share at least one common feature.

The items contained in a set are known as elements. We use the curled brackets to include the elements of the given set.

In math, we are mostly interested in number sets. We have the following number sets:

1. The set of natural numbers, N. In simpler words, this set includes only counting numbers, i.e. 1, 2, 3, . and so on. In symbols, we express the set of natural numbers as
   N = {1, 2, 3,}
   The three dots after the last element shown in the list indicate that the set continues to infinity.
2. The set of whole numbers, W. This set contains all natural (counting) numbers including zero. In symbols, we express the set of whole numbers as
   W = {0, 1, 2, 3,}
3. The set of integers, Z. This set contains all natural numbers, their opposite (the corresponding negative numbers) and zero. In symbols, we express the set of whole numbers as
   Z = {, -3, -2, -1, 0, 1, 2, 3, }
   The three dots on the left indicate that the set of integers is not restricted on the left, i.e. the negative integers extend to minus infinity, as well as positive integers that extend to plus infinity.
4. The set of rational numbers (fractions) Q. This set contains all fractions (both positive and negative) and is obtained by dividing an integer by a natural number. In symbols, we express the set of whole numbers as
   Q = {a/b, where a ϵ Z and b ϵ N}
   The symbol 'ϵ' means: "is an element of " and is used to indicate when an item is an element of a given set.
5. The set of irrational numbers, I. It includes all numbers that are not rational, i.e. those numbers that cannot be written as fractions. For example, the square root of all prime numbers, the Archimedes constant π, Euler's number e, etc., are all irrational numbers.
6. The set of real numbers, R. It includes all rational and irrational numbers.
7. The set of imaginary numbers i. This set includes all square roots of negative numbers, which in the set of real numbers normally do not exist. For example, √-5 is not defined in the set of real numbers but we can write it as i√5 in the set of imaginary numbers, where 'i' is the symbol used for 'imaginary', symbol i is used to replacing √-1 in an expression containing imaginary numbers.
8. The set of complex numbers, C. It includes all real and imaginary numbers. Complex numbers are written as a sum of a real and an imaginary number. For example, 3 - i√2 is a complex number, as it contains a real part (3) and an imaginary one (i√2, otherwise known as √-2).

We use the symbol '∈' to show that an element is a part of a given set. All sets are expressed in uppercase while elements of a set (when unknown) by lowercase. For example, a ∈ X means that a is an element of the set X. On the other hand, if an element b does not belong to the set X, we write the symbol '∉', which means 'not an element of'.

Some of the sets have a finite number of elements. They are known as finite sets. On the other hand, some of the sets have an infinity of elements. They are known as infinite sets. For example, all number sets from natural to complex, are infinite. We write three dots before the first or after the last element shown in the list.

There is a particular set, which does not contain any element, in analogy with the plastic bag used in the market, which has nothing inside before purchasing something. It is called the empty set and is denoted by the symbol ∅. We can write ∅ = { }. The empty set is also called a void set or null set. The existence of the empty set is necessary to prove some of the set properties. For example, this set is useful when trying to figure out all subsets we can form by the elements of a given set.

We call a subset any new set formed for the elements of a given set, including the empty set ∅. Likewise, the original set is considered a subset of itself.

It is not suitable to list all subsets of a given set when required. Therefore, we use the formula

to find the number N of all subsets formed by the elements of a set, where n [or n(A)] is the number of elements of the original set, otherwise known as the cardinal number of the given set A.

We use the symbol '⊆' to indicate that a given set A is a subset of another set B. In other words, if we write A ⊆ B we mean that all elements of set A are also elements of set B but the latter may contain more elements than the former.

The universal set U is the set where set A under consideration talks the values. Therefore, we can write A ⊆ U because the set A is a subset of the universal set U. For example, if we have the set A = {x ∈ N, x < 7}, the universal set U is the set of natural numbers N because A takes the values from N.

The set that has as its elements all subsets of a given set A is called the power set of A. We write it as P(A). These elements are all subsets we can form by combining the elements of A, including the empty set.

All the other subsets except the subset that includes all elements of the original set are called proper subsets while the subset that contains all elements of the original set is called an improper subset.

There are three methods used to represent sets. Depending on the situation discussed, each method offers its advantages and disadvantages to the other two. They are:

List method (Roaster method)

In this method, some (or all) elements of the set are written inside a pair of curled brackets as a list of numbers or other items, where each element is separated by a comma from the other elements of the given set. The general form of the list method representation is

The list must include as many elements as needed so that one may list correctly the rest of the elements (the part indicated by the three dots) in the set.

Defining-property(ies) method (Set-builder method)

The second method for representing sets is the defining-property(ies) method, otherwise known as the roaster method. In this method, all features that identify the set are written in symbols, separated by a comma. They are still listed inside the curled brackets as in the list methods but this time, no specific elements are written in the list but only the features that are sufficient to identify them.

You may encounter the following symbols when sets are expressed through the defining property method.

The symbol '∨' means 'or'. It is used to indicate that a condition applies in one of two possible situations. Thus, a = b ∨ a = c means a is equal to one of the values between b and c.

The symbol '∧' means 'and'. It is used to indicate that a condition applies in both of the two possible situations. Thus, a = b ∧ a = c means a is equal to b and c at the same time.

The symbol '→' means 'goes to'. It is used to indicate a condition that applies between two consecutive elements of a set.

The symbol '≡' means 'is equivalent to'. It is used when two sets have the same number of elements but not the same elements.

The symbol '/' means 'such that'. It often replaces the comma after the first condition when representing the set by means of the defining-property method.

Diagram Method

The third method of representing sets is called the diagram method, where the most common form is the Venn diagram, which is a kind of ellipse-shaped closed curve where all elements are spread out in different positions inside the shape.

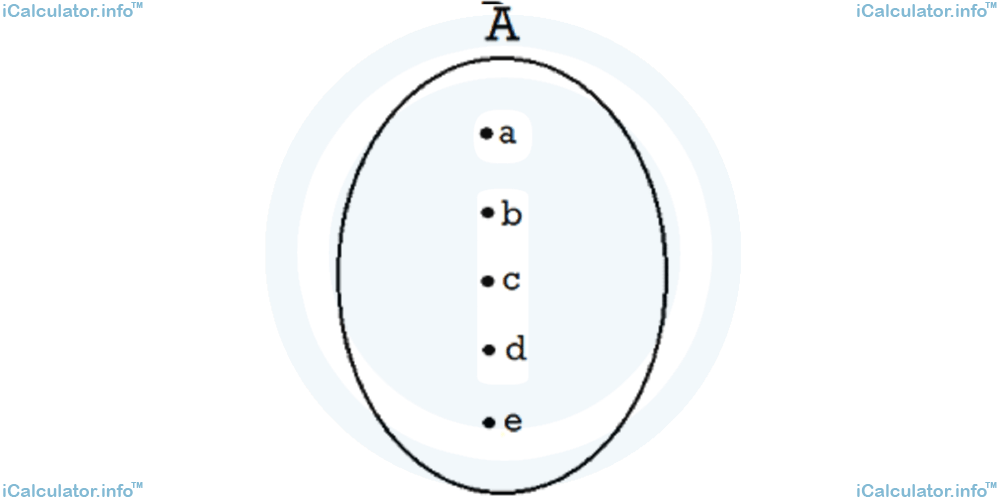
The elements a, b, c, d and e have a dot aside as a symbol that indicates the position of that specific element. In a certain sense, the diagram method has a similar structure to the list method but with a different design.

Sometimes, it is very helpful to compare the sets in order to have a better understanding of them. We have two types of such relationships between sets. Let's see them below.

Equivalent sets

Two sets are equivalent if they have the same number of elements. If A and B are equivalent, we write A ≡ B and say, 'set A is equivalent to set B'.

Equal sets

Two sets are equal if they have exactly the same elements. If A and B are equal, we write A = B, and say, 'set A is equal to set B.'

Different sets

If two sets A and B are not equivalent, then they are different.

Property: If two sets A and B are such that A ⊆ B and B ⊆ A, then A = B.

In other words, the above condition is observed when A is an improper subset of B and B is an improper subset of A.