Math Questions 16.2 - Injective, Surjective and Bijective Functions. Graphs of Functions

Please provide a rating, it takes seconds and helps us to keep this resource free for all to use

The following math revision questions are provided in support of the math tutorial on Injective, Surjective and Bijective Functions. Graphs of Functions. In addition to this tutorial, we also provide revision notes, a video tutorial, revision questions on this page (which allow you to check your understanding of the topic and calculators which provide full, step by step calculations for each of the formula in the Injective, Surjective and Bijective Functions. Graphs of Functions tutorials. The Injective, Surjective and Bijective Functions. Graphs of Functions calculators are particularly useful for ensuring your step-by-step calculations are correct as well as ensuring your final result is accurate.

Not sure on some or part of the Injective, Surjective and Bijective Functions. Graphs of Functions questions? Review the tutorials and learning material for Injective, Surjective and Bijective Functions. Graphs of Functions

Injective, Surjective and Bijective Functions. Graphs of Functions Revision Questions

1. . What is the domain of the function f(x) = 6 - 3√x?

1. [3, +∞)
2. [0, +∞)
3. [2, +∞)
4. (-∞, 0]

Reveal AnswerCorrect Answer: B

2. . Which of the following functions is injective?

1. f(x) = 3x - 2; X = {2, 4, 6, 8}; Y = {4, 10, 16, 22, 30}
2. f(x) = 3x - 2; X = {2, 4, 6, 8}; Y = {10, 16, 22}
3. f(x) = 3x - 2; X = {2, 4, 6, 8}; Y = {4, 10, 16, 24}
4. f(x) = 3x - 2; X = {2, 4, 6, 8}; Y = {6, 12, 18, 24}

Reveal AnswerCorrect Answer: B

3. . What is the codomain of the function shown in the figure?

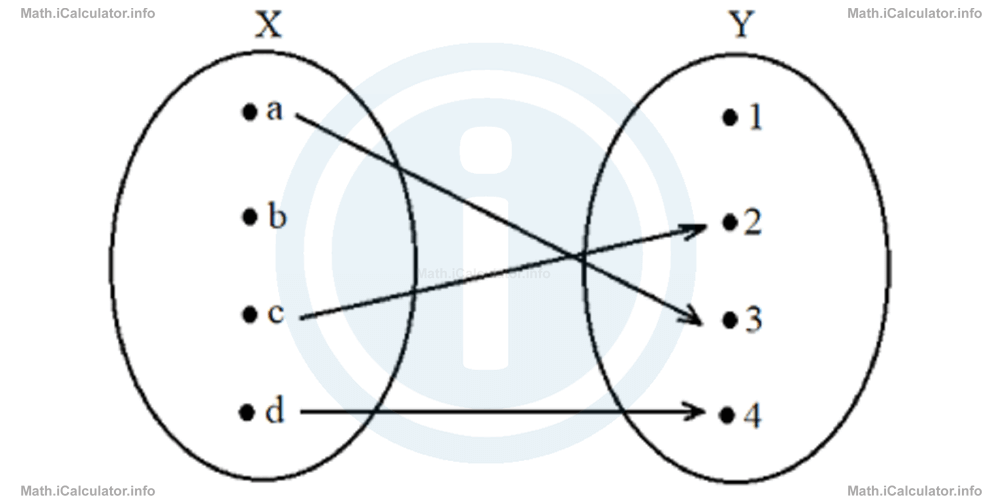
1. {a, b, c, d}
2. {a, c, d}
3. {1, 2, 3, 4}
4. {2, 3, 4}

Reveal AnswerCorrect Answer: C

4. . Which of the following functions is bijective?

1. f(x) = x² - 2x + 1
2. f(x) = 1 - x²
3. f(x) = 3x + 4
4. f(x) = x4

Reveal AnswerCorrect Answer: C

5. . Each of the output values of a bijective function is obtained by subtracting 5 from the triple of the corresponding input value. What is the formula of this function?

1. f(x) = 3x - 5
2. f(x) = 5 - 3x
3. f(x) = 5x + 3
4. f(x) = 5x - 3

Reveal AnswerCorrect Answer: A

6. . What can you say about line L shown in the figure below?

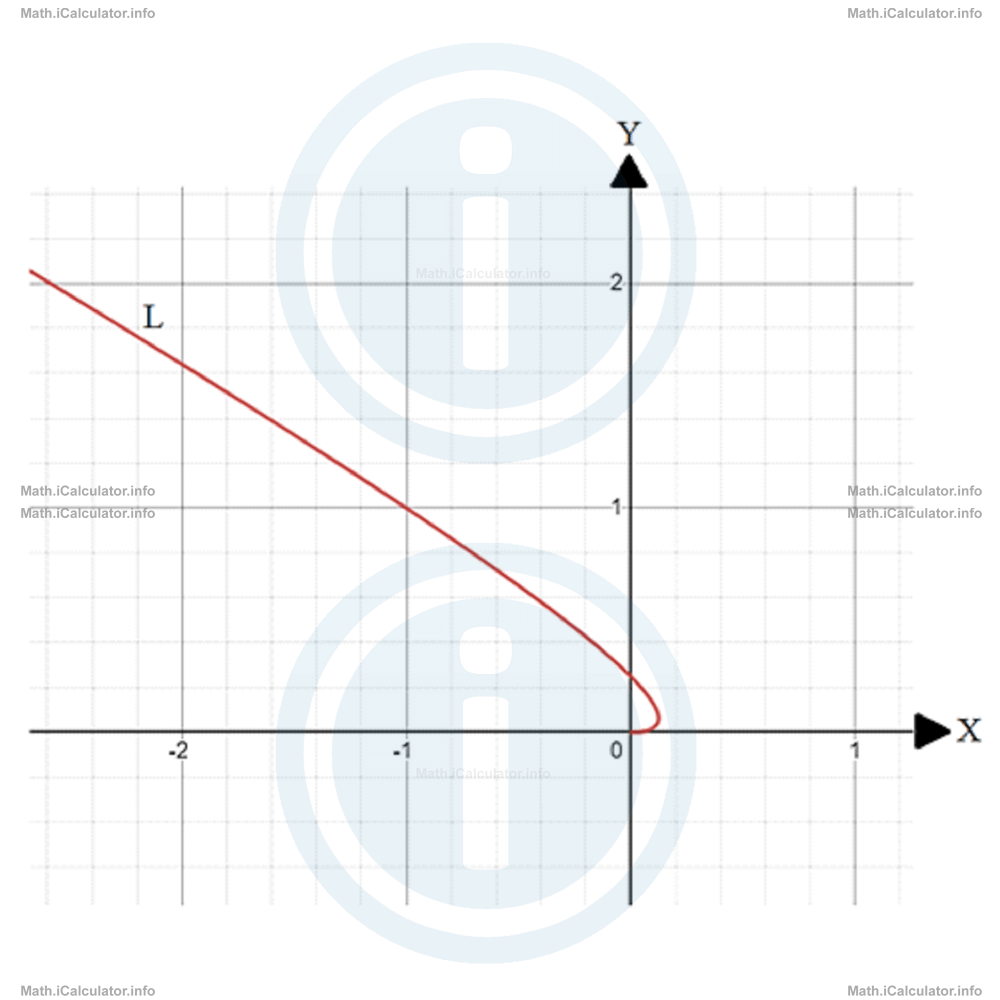
1. It shows an injective function
2. It shows a surjective function
3. It shows a bijective function
4. It does not represent a function

Reveal AnswerCorrect Answer: D

7. . In which of the following mathematical sentences the vertical line test produces two intercepts with the graph?

1. y=√(2x-5)
2. y²=2x
3. y=2x²
4. y=1/x²

Reveal AnswerCorrect Answer: B

8. . Which of the following mathematical sentences is NOT a function?

1. 3x² + y = 4
2. 2√x + 3x + y = 0
3. 5x + y² = 6
4. 5x + 5y = 1

Reveal AnswerCorrect Answer: C

9. . What is the range of the function f(x)=√(54-6x² )

1. R = (-∞, +∞)
2. R = [-3, 3]
3. R = [0, 3]
4. R = [0, 54]

Reveal AnswerCorrect Answer: D

10. . The horizontal line test is useful in which of the following lines?

1. x² + y² = 9
2. x² + √y = 1
3. x + y² = 4
4. x² - y² = 5

Reveal AnswerCorrect Answer: B

Whats next?

Enjoy the "Injective, Surjective and Bijective Functions. Graphs of Functions" practice questions? People who liked the "Injective, Surjective and Bijective Functions. Graphs of Functions" practice questions found the following resources useful:

1. Practice Questions Feedback. Helps other - Leave a rating for this practice questions (see below)
2. Functions Math tutorial: Injective, Surjective and Bijective Functions. Graphs of Functions. Read the Injective, Surjective and Bijective Functions. Graphs of Functions math tutorial and build your math knowledge of Functions
3. Functions Revision Notes: Injective, Surjective and Bijective Functions. Graphs of Functions. Print the notes so you can revise the key points covered in the math tutorial for Injective, Surjective and Bijective Functions. Graphs of Functions
4. Check your calculations for Functions questions with our excellent Functions calculators which contain full equations and calculations clearly displayed line by line. See the Functions Calculators by iCalculator™ below.
5. Continuing learning functions - read our next math tutorial: Basic Functions

Help others Learning Math just like you

Please provide a rating, it takes seconds and helps us to keep this resource free for all to use

We hope you found this Math tutorial "Injective, Surjective and Bijective Functions. Graphs of Functions" useful. If you did it would be great if you could spare the time to rate this math tutorial (simply click on the number of stars that match your assessment of this math learning aide) and/or share on social media, this helps us identify popular tutorials and calculators and expand our free learning resources to support our users around the world have free access to expand their knowledge of math and other disciplines.

Functions Calculators by iCalculator™