Math Lesson 16.5.4 - Piecewise Functions with More than Two Parts

Please provide a rating, it takes seconds and helps us to keep this resource free for all to use

Welcome to our Math lesson on Piecewise Functions with More than Two Parts, this is the fourth lesson of our suite of math lessons covering the topic of Piecewise Functions, you can find links to the other lessons within this tutorial and access additional Math learning resources below this lesson.

Piecewise Functions with More than Two Parts

Piecewise functions may contain more than two parts but the approach used is the same as above. The only difference is that we must have to check the function's continuity (if required) at more than one point.

As for the graph, we sketch the graph of each individual function in its domain and then look for any common point. It is worth pointing out the fact that if any piece of such function does not include an endpoint, we represent this endpoint on the graph through a blank dot. However, if the function is continuous, this blank dot is filled by the endpoint of the other piece of the original function.

Example 4

For the piecewise-defined function below

find:

1. Domain and range
2. f(-3), f(0), f(1) and f(4)
3. Check the continuity at x = 0 and x = 2
4. Plot the graph of this function

Solution 5

1. None of the function pieces contain any square root, fraction or logarithm that could possibly limit the choice for the values of x. therefore, the domain of f(x) is the whole set of real numbers R.
   As for the range, we consider the pieces one by one. Thus, the upper piece cannot be 0 or more because x^x is always positive or zero. The negative sign before x^x makes this part always negative.
   The middle piece has a range that extends from 0 (including it) to 4 (without including it) given that f(x) = 2x and the independent variable x ranges from 0 to 2.
   The bottom piece ranges from 2 (including it) to positive infinity given that f(x) = 3x - 4 and the minimum value of the domain for this part of the function is x = 2. Thus, f(2) = 3 · 2 - 4 = 2.
2. We have to consider the upper part of the function to calculate f(-3) given that -3 belongs to the domain of this part of the function. Thus,
   f(x) = -x²
   f(-3) = -(-3)²
   = -9
   We have to consider the middle part of the function to calculate f(0) given that 0 belongs to the domain of this part of the function. Thus,
   f(x) = 2x
   f(0) = 2 ∙ 0
   = 0
   We have to consider again the middle part of the function to calculate f(1) given that 1 belongs to the domain of this part of the function. Thus,
   f(x) = 2x
   f(1) = 2 ∙ 1
   = 2
   We have to consider the bottom part of the function to calculate f(2) given that 2 belongs to the domain of this part of the function. Thus,
   f(x) = 3x - 2
   f(2) = 3 ∙ 2 - 2
   = 6 - 2
   = 4
3. To check the continuity of the function at x = 0 we must find f(0) for the upper and middle parts and compare the values obtained. If they are equal, the function is continuous at that point. Thus, for the upper part, we have
   f(0) = -0²
   = 0
   and for the middle part, we have
   f(0) = 2 ∙ 0
   = 0
   Therefore, the function is continuous at x = 0.
   We follow the same procedure for x = 2. This time we have to consider the middle and the bottom part of the function. Thus, for the middle part, we have
   f(2) = 2 ∙ 2
   = 4
   and for the bottom part, we have
   f(2) = 3 ∙ 2 - 2
   = 6 - 2
   = 4
   Therefore, the function is continuous at x = 2.
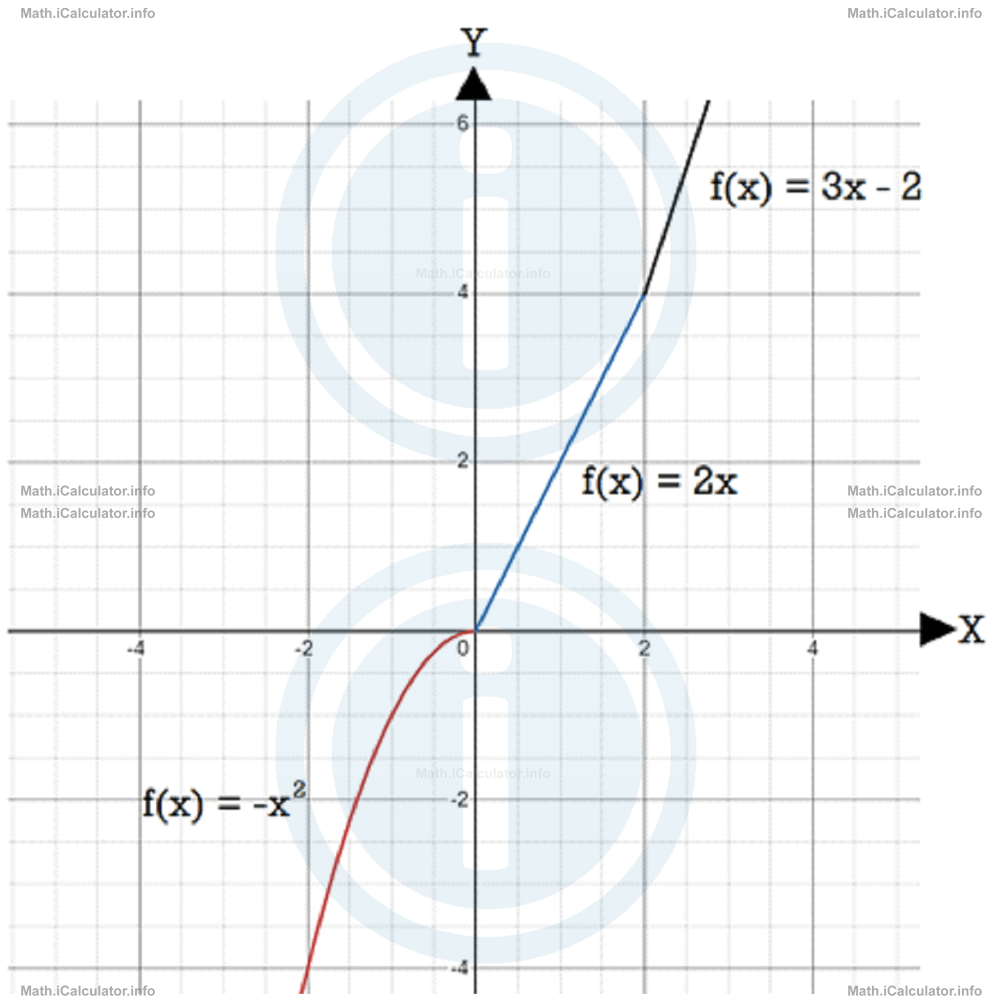
4. The graph will have three different parts, one for each piece. The left part extends from minus infinity to 0. It is a curve (parabola), which has a maximum and the arms down. Only the left branch of the parabola appears on the graph given that it cannot extend to the positive direction of the X-axis. On the other hand, the middle and the right parts are both straight lines with different steepness based on their corresponding gradients. The middle part extends from x = 0 to x = 2 while the right part extends from x = 2 to plus infinity. Look at the figure below (each piece is shown with a different colour for more clarity).

You have reached the end of Math lesson 16.5.4 Piecewise Functions with More than Two Parts. There are 6 lessons in this physics tutorial covering Piecewise Functions, you can access all the lessons from this tutorial below.

More Piecewise Functions Lessons and Learning Resources

Whats next?

Enjoy the "Piecewise Functions with More than Two Parts" math lesson? People who liked the "Piecewise Functions lesson found the following resources useful:

1. Two Parts Feedback. Helps other - Leave a rating for this two parts (see below)
2. Functions Math tutorial: Piecewise Functions. Read the Piecewise Functions math tutorial and build your math knowledge of Functions
3. Functions Revision Notes: Piecewise Functions. Print the notes so you can revise the key points covered in the math tutorial for Piecewise Functions
4. Functions Practice Questions: Piecewise Functions. Test and improve your knowledge of Piecewise Functions with example questins and answers
5. Check your calculations for Functions questions with our excellent Functions calculators which contain full equations and calculations clearly displayed line by line. See the Functions Calculators by iCalculator™ below.
6. Continuing learning functions - read our next math tutorial: Inverse Functions

Help others Learning Math just like you

Please provide a rating, it takes seconds and helps us to keep this resource free for all to use

We hope you found this Math tutorial "Piecewise Functions" useful. If you did it would be great if you could spare the time to rate this math tutorial (simply click on the number of stars that match your assessment of this math learning aide) and/or share on social media, this helps us identify popular tutorials and calculators and expand our free learning resources to support our users around the world have free access to expand their knowledge of math and other disciplines.

Functions Calculators by iCalculator™