Math Lesson 7.4.1 - What Are Surds?

Welcome to our Math lesson on What Are Surds?, this is the first lesson of our suite of math lessons covering the topic of Surds, you can find links to the other lessons within this tutorial and access additional Math learning resources below this lesson.

What Are Surds? What is the Difference between Surds and Transcendental and Irrational Numbers?

When the term "surds" was first introduced, mathematicians intended it as an alternative name for irrational numbers. So, basically, in that original sense, they considered surds and irrational numbers as representing the same thing.

However, now surds and irrational numbers mean different things. More precisely, surds represent only a subset of irrational numbers. This means there are many irrational numbers that are not surds but on the other hand, all surds are irrational numbers.

Let's explain in more detail the difference between surds and irrational numbers by introducing the subset of irrational numbers that do not belong to surds. All numbers included in this subset are called 'transcendental numbers' and we may encounter them in the form of constants used in science. For example, π, e (Euler's Number), trigonometric functions such as sin α, cos α, tan α and cot α if the angle is measured in radians, etc., are all transcendental numbers.

By definition, a transcendental number is an irrational number that is not the root of any number, meaning that it is not an algebraic number of any degree.

From here, by induction, we obtain the definition of surds. Thus, surds are all numbers representing unresolved roots of any real number.

For example, √2;√3; √8; ∛11; √29; √1/6; etc., are all surds because their value (although irrational) is obtained by calculating the roots of either integers or rational numbers (integers are rational numbers though). Indeed, when a calculator is used to find the value of the above numbers, it gives

On the other hand, numbers like √25; √2.8224; ∛0.125; etc., are not surds because the result of these roots is a finite number. Indeed,

and

The following diagram shows the relationship between surds, transcendental numbers and irrational ones.

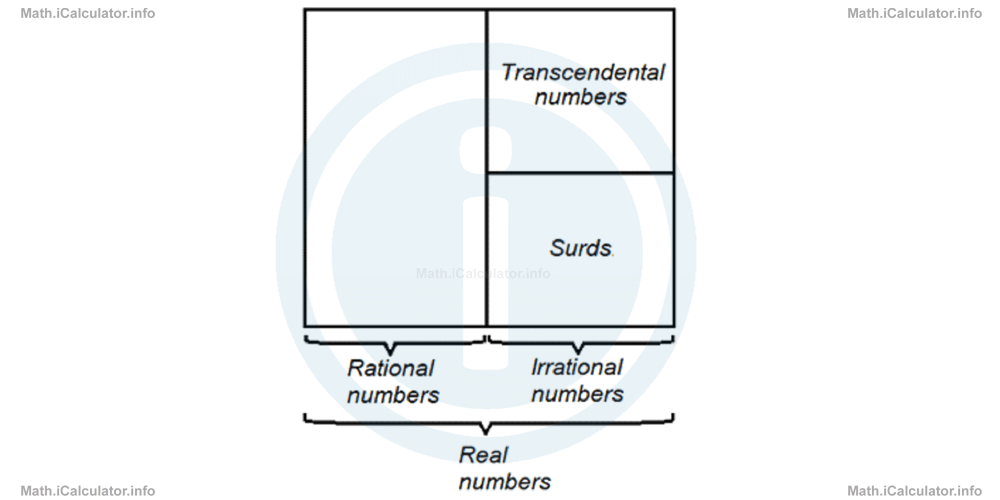
To summarize, a surd is a root of a positive real quantity if its value cannot be exactly determined.

Example 1

Which of the following numbers represents a surd?

1. √121
2. ∛125
3. √179.56
4. √21

Solution 1

Using a calculator to make the operations, we obtain

1. √121 = 11
2. ∛125 = 5
3. √179.56 = 13.4
4. √21 = 4.582575694955840006588047193728…

From all numbers, only √21 gives an infinite non-recurring part after the decimal point. All the other roots are finite, so they are not surds. Only √21 is a surd.

More Surds Lessons and Learning Resources

Whats next?

Enjoy the "What Are Surds?" math lesson? People who liked the "Surds lesson found the following resources useful:

1. What Feedback. Helps other - Leave a rating for this what (see below)
2. Powers and Roots Math tutorial: Surds. Read the Surds math tutorial and build your math knowledge of Powers and Roots
3. Powers and Roots Video tutorial: Surds. Watch or listen to the Surds video tutorial, a useful way to help you revise when travelling to and from school/college
4. Powers and Roots Revision Notes: Surds. Print the notes so you can revise the key points covered in the math tutorial for Surds
5. Powers and Roots Practice Questions: Surds. Test and improve your knowledge of Surds with example questins and answers
6. Check your calculations for Powers and Roots questions with our excellent Powers and Roots calculators which contain full equations and calculations clearly displayed line by line. See the Powers and Roots Calculators by iCalculator™ below.
7. Continuing learning powers and roots - read our next math tutorial: Rationalising the Denominator

Help others Learning Math just like you

We hope you found this Math tutorial "Surds" useful. If you did it would be great if you could spare the time to rate this math tutorial (simply click on the number of stars that match your assessment of this math learning aide) and/or share on social media, this helps us identify popular tutorials and calculators and expand our free learning resources to support our users around the world have free access to expand their knowledge of math and other disciplines.

Powers and Roots Calculators by iCalculator™

• Expressing Ordinary Numbers In Standard Form Calculator
• Multiplication And Division Of Roots Calculator
• Operations With Standard Numbers Calculator