Menu
Math Lesson 12.1.4 - A fast method for Finding the nth Term of a Sequence
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
Welcome to our Math lesson on A fast method for Finding the nth Term of a Sequence, this is the fourth lesson of our suite of math lessons covering the topic of Working with Term-to-Term Rules in Sequences, you can find links to the other lessons within this tutorial and access additional Math learning resources below this lesson.
How to find the nth Term of a Sequence in a more efficient way
Although sequence notation is more suitable to represent the terms of a number sequence compared to the list method described earlier, we are not fully satisfied, as still, we have to calculate the terms one by one to get to the desired term.
In some sequences, however, it is possible to identify formulas that allow us to calculate the nth term of a sequence (xn) based on the first term x1 without using the (long) recurrent procedure described earlier. Let's explain how to find the nth term in two widespread sequences: arithmetic and geometric.
1. Finding the nth term in an arithmetic sequence
Earlier in this tutorial, we have explained that in an arithmetic sequence the difference d between two consecutive terms is always constant. Thus, denoting the first term of such a sequence by x1 and the general term by xn, we can write:
x3 = x2 + d = (x1 + d) + d = x1 + 2d
x4 = x3 + d = (x1 + 2d) + d = x1 + 3d
⋮
Hence, after n recurring operations, we obtain the general term xn of an arithmetic sequence in terms of the difference d and the first term x1:
Thus, if for example, we have the first term of an arithmetic sequence x1 = -9 and the common difference d = 7 given, we can effortlessly calculate whatever term of this sequence we want, no matter how far from the first term in the list it is. For example, the 108th term of this sequence (n = 108) is
x108 = -9 + (108 - 1) ∙ 7
= -9 + 107 ∙ 7
= -9 + 749
= 740
(If you have doubts, try to solve the exercise by the recurring method J)
Example 7
The fourth term of an arithmetic sequence is 17 and the ninth term of the same sequence is 32.
- Find the first term of this sequence
- Find the 86th term of the same sequence
Solution 7
- First, let's calculate the common difference d. We have x4 = 17 and x9 = 32. We get from x4 to x9 by adding 5 times the common difference, as the ninth term is 5 terms away from the fourth one. Hence, x9 = x4 + 5dNow, we can find the first term (x1) by using the same procedure. Since x4 is 3 terms away from x1, we obtain
x9 - x4 = 5d
d = x9 - x4/5
= 32 - 17/5
= 15 /5
= 3x4 = x1 + 3d
x1 = x4-3d
x1 = 17 - 3 ∙ 3
= 17 - 9
= 8 - As for the 86th term of the sequence (n = 86), we have xn = x1 + (n - 1) ∙ d
x86 = 8 + (86 - 1) ∙ 3
= 8 + 85 ∙ 3
= 8 + 255
= 263
It is also possible to find the nth term of arithmetic sequences in cases similar to the above by solving a system of linear equations. For some people, this method may seem more suitable. Thus, since
we can write
and
Solving the system of linear equations obtained yields
Multiplying the first equation by -1 to eliminate x1 yields
15 = 5d
d = 3
Hence,
17 = x1 + 9
x1 = 8
The rest of the solution used for finding x86 is the same as in the previous solution.
2. Finding the nth term in a geometric sequence
We can use the same approach as above in identifying a general formula for finding the nth term of a geometric sequence (xn) when the first term x1 and the common ratio R are given. Thus, since
x3 = x2 ∙ R = (x1 ∙ R) ∙ R = x1 ∙ R2
x4 = x3 ∙ R = (x1 ∙ R2 ) ∙ R = x1 ∙ R3
⋮
we obtain the formula for the general term xn of a geometric sequence
For example, if the first term of a geometric sequence is 3 (x1 = 3) and the common ratio is 2 (R = 2), then the 12th term (x12) of this sequence (n = 12) is
x12 = 3 ∙ 212 - 1
= 3 ∙ 211
= 3 ∙ 2048
= 6144
Example 8
The first term of a geometric sequence is 81 and the common ratio is 1/3. Calculate the 8th term of this sequence.
Solution 8
We have x1 = 81, R = 1/3 and n = 8. Thus, given the formula for the general term of a geometric sequence
we obtain for the eighth term of this sequence
= 34 ∙ (1/3)7
= 34 ∙ 3-7
= 34 - 7
= 3-3
= 1/33
= 1/27
3. Finding the nth term of combined sequences
When a sequence is a combination of two or more types of sequences described above, the general term is calculated by considering each component sequence separately. For example, in the sequence
there is a combination of an arithmetic sequence (in the numerator) and a geometric one (in the denominator). Therefore the nth term of this combined sequence is calculated in two steps: one for the numerator and the other for the denominator. For example, if we want to find the 14th term of this sequence, we follow the procedure below:
The 14th numerator = x14, where x1 = 1, d = 2 and n = 14. Thus,
x14 = 1 + (14 - 1) ∙ 2
= 1 + 13 ∙ 2
= 1 + 26
= 27
The 14th denominator = y14, where y1 = 2, R = 2 and n = 14. Thus,
y14 = 2 ∙ 214 - 1
= 2 ∙ 213
= 214
= 16,384
Therefore, the 14th term (T14) of the given sequence is
Example 9
Calculate the 11th term of the number sequence
Solution 9
The numerators form an arithmetic sequence where the first term is x1 = 4 and the common difference is d = -3, while the denominators form a geometric sequence where the first term is y1 = 128 and the common ratio is R = 1/4. Hence, the 11th term in each sequence (n = 11) will be
x11 = 4 + (11 - 1) ∙ (-3)
= 4 + 10 ∙ (-3)
= 4 - 30
= -34
and
y11 = 128 ∙ (1/4)11 - 1
= 128 ∙ (1/4)10
= 128 ∙ 110/410
= 128 ∙ 1/1,048,576
= 1/8192
Therefore, we have for the 11th term T11 of the original fractional sequence
= -34/1/8192
= -34/1 ∙ 8192/1
= -278,528
4. Finding the nth term of quadratic sequences
As we explained earlier, in quadratic sequences the difference between two consecutive terms changes by the same amount each time when moving from left to right. Therefore, it is important to find this change of differences (i.e. the second difference), as it is constant and can be processed easier.
Since such sequences are called "quadratic", they must have many things in common with quadratic equations. In fact, we saw earlier in this tutorial that terms change from each other in a quadratic polynomial fashion. Indeed, the nth term of a quadratic sequence is of the type
where a, b and c are constants (a ≠ 0), while n represents the number of the term giving that the difference between consecutive terms is not constant and therefore, we cannot rely on the common difference d anymore.
There is a standard procedure used to find the nth term of a quadratic sequence, explained below.
Step 1: Find the constant second difference of the given quadratic sequence.
Step 2: Divide that number by 2 to obtain the coefficient a.
Step 3: Subtract the term an2 from each known term of the quadratic expression an2 + bn + c. The remaining expression is therefore linear.
Step 4: Calculate the nth term of this linear sequence. This gives bn + c.
Step 5: Substitute all values found above in the original quadratic expression.
For example, in the quadratic sequence 6, 13, 26, 45, …, the difference between consecutive terms increases by 6 every time we shift from left to right, as
x3 - x2 = 26 - 13 = 13 = 7 + 6
x4 - x3 = 45 - 26 = 19 = 13 + 6
and so on. Therefore, the coefficient a in the quadratic expression an2 + bn + c is
Hence, the value of an2 for the four known terms of the original quadratic sequence (i.e. for n = 1, 2, 3 and 4) is
For n = 1, the value of 3n2 is: 3n12 = 3 · 12 = 3 · 1 = 3.
For n = 2, the value of 3n2 is: 3n22 = 3 · 22 = 3 · 4 = 12.
For n = 3, the value of 3n2 is: 3n32 = 3 · 32 = 3 · 9 = 27.
For n = 4, the value of 3n2 is: 3n42 = 3 · 42 = 3 · 16 = 48.
Therefore, the difference between the original term and the corresponding an2 terms obtained above, which gives the first four terms of the new linear sequence, isT2 = x2 - an22 = 13 - 12 = 1
T3 = x3 - an23 = 26 - 27 = -1
T4 = x4 - an24 = 45 - 48 = -3
In this way, we obtain the linear sequence 3, 1, -1, -3, …; where the first term is T1 = 3 and the common difference is d = -2. Hence, the general expression for the nth term in this new arithmetic sequence is
= 3 + (n - 1) ∙ (-2)
= 3 + (-2n + 2)
= 3 - 2n + 2
= -2n + 5
This is the (bn + c) part in the original quadratic sequence expressed in terms of n. Hence, we obtain
This expression allows us to calculate whichever term of the original quadratic sequence we want. For example, the 24th term of this sequence (n = 24) is
x24 = 3 ∙ 242-2 ∙ 24 + 5
= 3 ∙ 576 - 2 ∙ 24 + 5
= 1728 - 48 + 5
= 1685
Example 10
Find the 34th term of the sequence
Solution 10
Carefully look at the difference between two consecutive terms. First, it decreases by 2, then it remains constant, then increases by 2, by 4, by 6 and so on. Therefore, the change in difference increases by 2 every time we move from left to right. This means we are dealing with a quadratic sequence, where the general term has the form
Hence, since the coefficient a is half of the change in the differences, i.e. a = 2/2 = 1.
For convenience, we can create a table where all the necessary information as explained in theory is included.
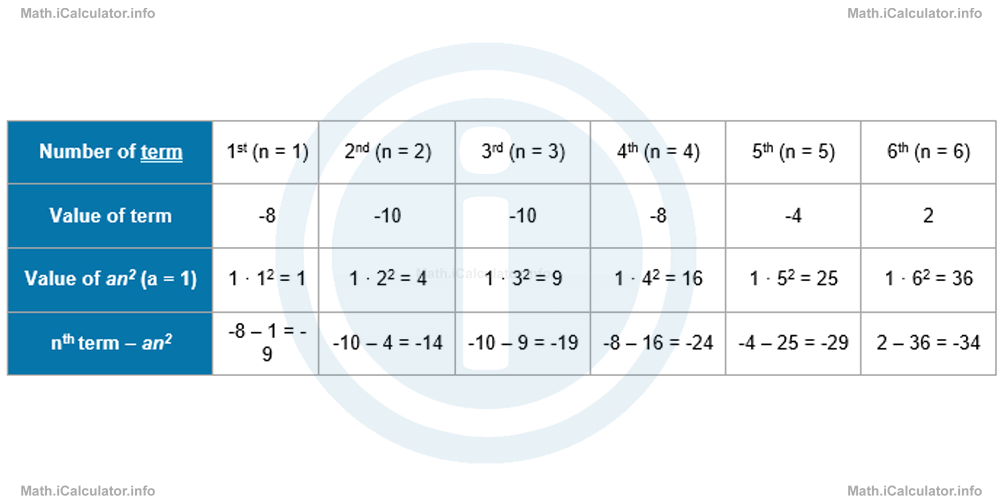
In this way, we obtained the linear (arithmetic) sequence
where the first term T1 = -9 and the common difference d = -5. Hence, we obtain the general term Tn of this arithmetic sequence, which gives the (bn + c) part of the quadratic sequence when expressed in terms of n:
= T1 + (n - 1) ∙ d
= -9 + (n - 1) ∙ (-5)
= -9 + (-5n + 5)
= -9 - 5n + 5
= -5n-4
Therefore, the quadratic general term xn is
= n2 - 5n - 4
Now, we are ready to find the 34th term of the original sequence (n = 34). Thus,
x34 = 342 - 5 ∙ 34 - 4
= 1156 - 170 - 4
= 982
More Working with Term-to-Term Rules in Sequences Lessons and Learning Resources
Whats next?
Enjoy the "A fast method for Finding the nth Term of a Sequence" math lesson? People who liked the "Working with Term-to-Term Rules in Sequences lesson found the following resources useful:
- Fast Nth Term Sequence Feedback. Helps other - Leave a rating for this fast nth term sequence (see below)
- Sequences and Series Math tutorial: Working with Term-to-Term Rules in Sequences. Read the Working with Term-to-Term Rules in Sequences math tutorial and build your math knowledge of Sequences and Series
- Sequences and Series Video tutorial: Working with Term-to-Term Rules in Sequences. Watch or listen to the Working with Term-to-Term Rules in Sequences video tutorial, a useful way to help you revise when travelling to and from school/college
- Sequences and Series Revision Notes: Working with Term-to-Term Rules in Sequences. Print the notes so you can revise the key points covered in the math tutorial for Working with Term-to-Term Rules in Sequences
- Sequences and Series Practice Questions: Working with Term-to-Term Rules in Sequences. Test and improve your knowledge of Working with Term-to-Term Rules in Sequences with example questins and answers
- Check your calculations for Sequences and Series questions with our excellent Sequences and Series calculators which contain full equations and calculations clearly displayed line by line. See the Sequences and Series Calculators by iCalculator™ below.
- Continuing learning sequences and series - read our next math tutorial: Working with Arithmetic and Geometric Series. How to find the Sum of the First n-Terms of a Series.
Help others Learning Math just like you
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
We hope you found this Math tutorial "Working with Term-to-Term Rules in Sequences" useful. If you did it would be great if you could spare the time to rate this math tutorial (simply click on the number of stars that match your assessment of this math learning aide) and/or share on social media, this helps us identify popular tutorials and calculators and expand our free learning resources to support our users around the world have free access to expand their knowledge of math and other disciplines.