Math Lesson 12.1.2 - The Different Types of Sequences Explained

Please provide a rating, it takes seconds and helps us to keep this resource free for all to use

Welcome to our Math lesson on The Different Types of Sequences Explained, this is the second lesson of our suite of math lessons covering the topic of Working with Term-to-Term Rules in Sequences, you can find links to the other lessons within this tutorial and access additional Math learning resources below this lesson.

Different Types of Sequences

In this section, we will briefly explain some types of sequences. We use the so-called "Term-to-Term Rules" to get from one term of a sequence to another.

1. Arithmetic Sequences

An arithmetic sequence (otherwise known as "arithmetic progression") is a type of number sequence where the difference between two consecutive terms is always the same. Arithmetic sequences are also known as linear sequences. For example,

is an arithmetic sequence, as x₁ = 1, x₂ = 4, x₃ = 7, x₄ = 10, x₅ = 13, etc., so the difference between two consecutive terms is always constant (x_n - x_n - 1 = 3). Hence, the pattern of this sequence is "add by 3."

If the difference between two consecutive terms in an arithmetic sequence is positive the terms are increasing, otherwise, they are decreasing (for example, 19, 15, 11, …, where a_n - a_{n - 1} = -4). The pattern of this sequence is "subtract by 4."

The difference between two consecutive terms in an arithmetic sequence is known as the common difference, d. In the first arithmetic sequence, we have d = 3 while in the second arithmetic sequence d = -4.

2. Geometric Sequences

A geometric sequence (otherwise known as "geometric progression") is a type of number sequence where the ratio between two consecutive terms is always the same. For example,

is a geometric sequence, as a₁ = 2, a₂ = 6, a₃ = 18, a₄ = 54, a₅ = 162, etc., so a_n/a_{n - 1} = 3. The pattern of this sequence therefore is "multiply by 3."

Like in arithmetic sequences, if the ratio between two consecutive terms in a geometric sequence is positive the terms are increasing, otherwise, they are decreasing (for example, 80, 40, 20, …, where an/an-1 = 1/2). The pattern of this sequence, therefore, is "divide by 2" or "multiply by 1/2."

The ratio between two consecutive terms in a geometric sequence is known as the common ratio, R. In the first geometric sequence we have R = 3 while in the second geometric sequence R = 1/2.

Example 2

Determine the type of sequence and the pattern in the number sequences below.

1. -3, -8, -13, -18, …
2. -4, -1, 2, 5, 8, …
3. 4, 2, 1, 1/2, 1/4, …
4. 4, 20, 100, 500, …

Then, find the next three terms in each sequence.

Solution 2

1. This is an arithmetic sequence because the terms decrease by 5 when moving from left to right. The pattern, therefore, is "subtract 5 from the previous term." The difference d between two consecutive terms is d = -5. Moreover, this is an infinite sequence, as it has a beginning (-3) but no end. Following the given pattern, we find the next three terms. They are highlighted in yellow, as shown below.
   -3, -8, -13, -18, -23, -28, -33, …
2. This is an arithmetic sequence because the terms increase by 3 when moving from left to right. The pattern, therefore, is "add 3 to the previous term." The difference d between two consecutive terms is d = 3. Moreover, this is an infinite sequence, as it has a beginning (-4) but no end. Following the given pattern, we find the next three terms. They are highlighted in yellow, as shown below.
   -4, -1, 2, 5, 8, 11, 14, 17, …
3. This is a geometric sequence because the terms increase by a factor of 5 when moving from left to right. The pattern, therefore, is "multiply by 5 the previous term." The ratio R between two consecutive terms is R = 5. Moreover, this is an infinite sequence, as it has a beginning (4) but no end. Following the given pattern, we find the next three terms. They are highlighted in yellow, as shown below.
   4, 2, 1, 1/2, 1/4, 1/8, 1/16, 1/32…
4. This is a geometric sequence because the terms halve when moving from left to right. The pattern, therefore, is "divide by 2 the previous term." The ratio R between two consecutive terms is R = 1/2. Moreover, this is an infinite sequence, as it has a beginning (4) but no end. Following the given pattern, we find the next three terms. They are highlighted in yellow, as shown below.
   4, 20, 100, 500, 2500, 12500, 62500…

3. Fibonacci-Type Sequences

A Fibonacci-type sequence is a particular kind of number sequence where the next term is obtained by adding the previous two terms. In symbols, a Fibonacci sequence is expressed as x_n = x_n - 2 + x_n - 1.

For example,

is a Fibonacci-type sequence, as 0 + 1 = 1, 1 + 1 = 2, 1 + 2 = 3, 2 + 3 = 5, and so on.

Example 3

Find the values of x, y and z in the Fibonacci-type sequence below.

Solution 3

Since each term of the sequence is obtained by adding the previous two, we have

Thus x = 10.

Yet,

Thus, y = 16.

Moreover,

Thus, z = 42.

4. Quadratic Sequences

Quadratic sequences are those sequences in which the difference between two consecutive terms changes by the same amount each time when moving from left to right. For example, the sequence

is a quadratic sequence, as the difference between two consecutive terms increases by 2 each time we move from left to right.

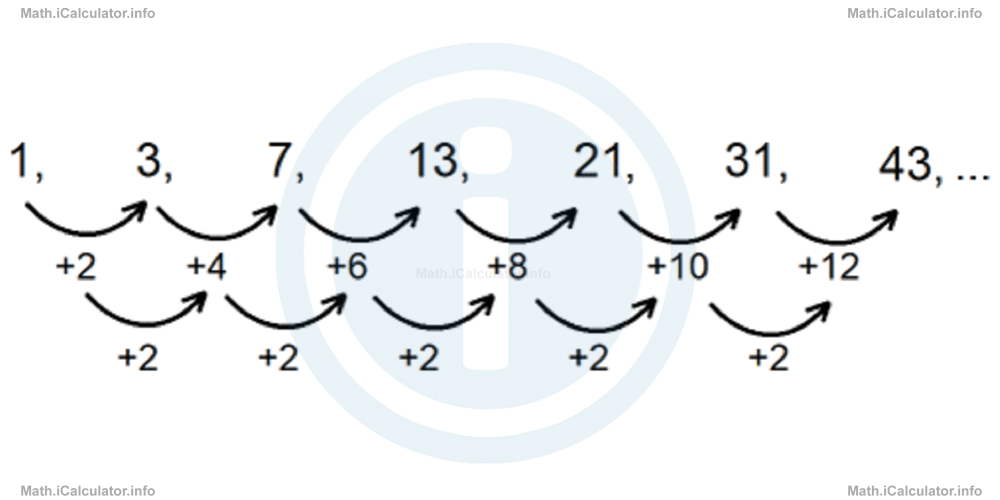
Such sequences are called quadratic because they follow the pattern of quadratic polynomials/functions, where the difference between two consecutive terms changes by the same value. For example, in the polynomial P(x) = x² the values of P(1), P(2), P(3) and P(4) are 1, 4, 9 and 16 respectively. You can see that the difference between two consecutive terms increases by 2 each time we shift to a higher value of the variable x.

Example 4

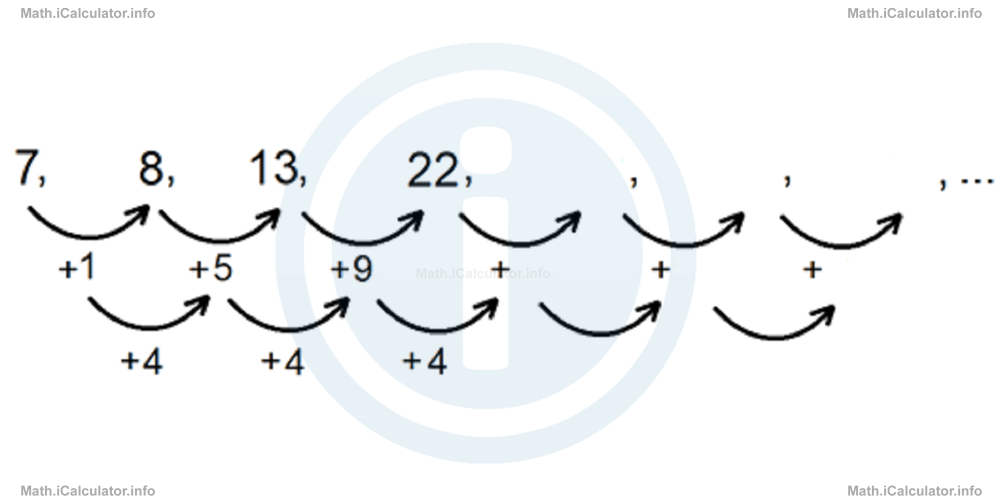
The sequence

is a quadratic one. Calculate the next three terms of this sequence.

Solution 4

This is a quadratic sequence, as the difference between two consecutive terms increases by 4 when moving from left to right. This means the sequence has the following pattern:

Continuing this pattern with other three terms yields

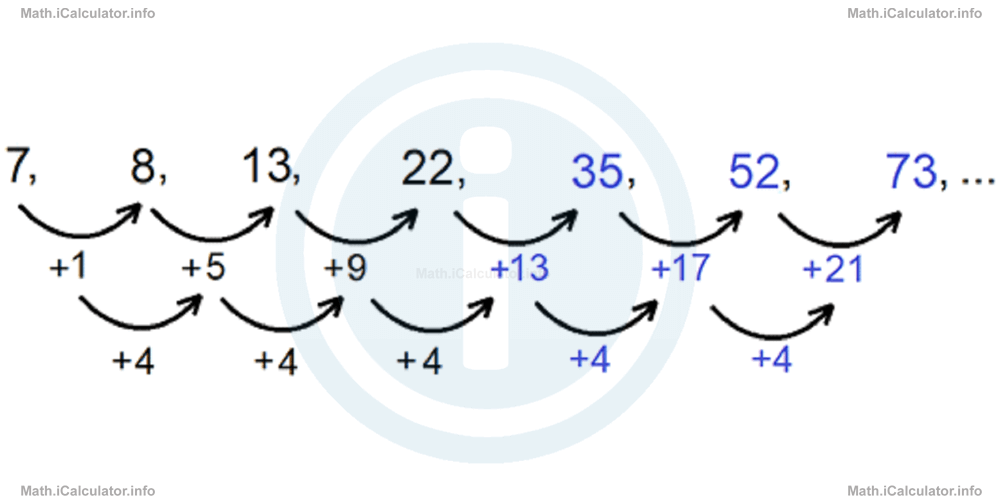
Figure-Like Sequences

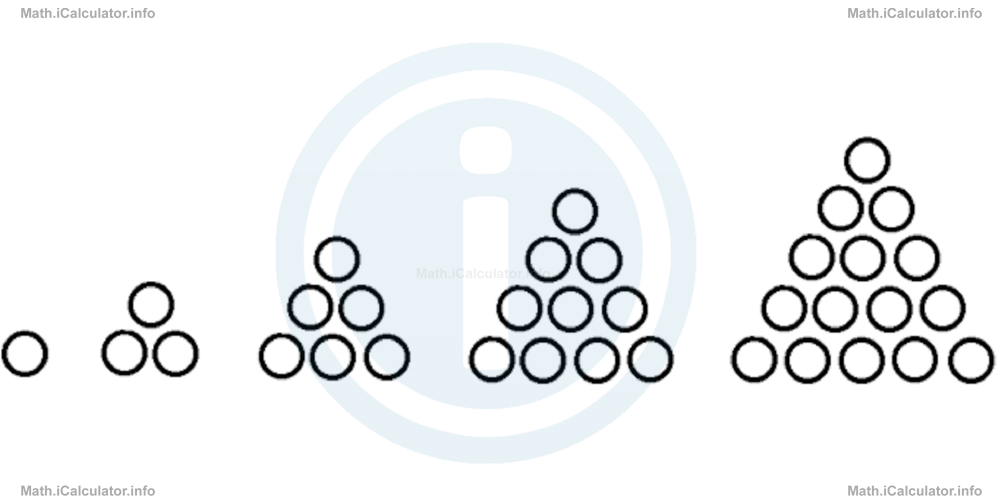
Sometimes, the patterns that certain sequences follow are similar to certain geometrical shapes. For example, the sequence

looks like equilateral triangles formed by small balls that increase in size when moving from left to right, as shown in the figure below.

Another sequence that has a figure-like pattern is

which has a visual appearance as shown below.

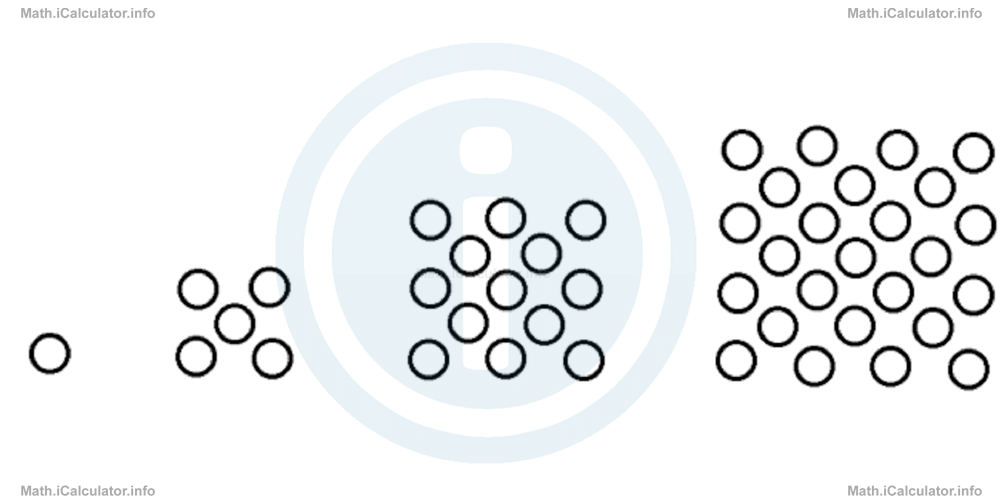
and so on.

5. Shape Sequences

Shape patterns can form sequences when they have some regularity. The most common shape sequences involve the enlargement or reduction of shapes' size according to a given rule. Look at the figure below.

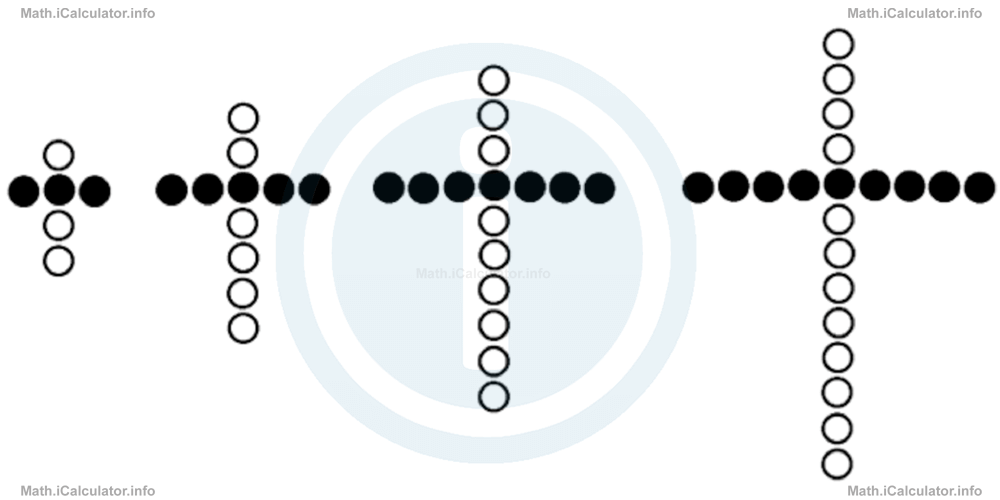
We can identify two different patterns in this figure: the pattern of the black circles and that of the white circles. You can easily find that the pattern of black circles is "add by two" and that of white circles is "add by three". Therefore, we have two arithmetic sequences in the same figure:

Moreover, we can obtain other sequences with specific parts of the figure. For example, with the bottom part of the shapes in the figure, we can form the numbers sequence 2, 4, 6, 8; with the upper part, we have the sequence 1, 2, 3, 4. The same for the left or right parts alone.

Example 5

1. Write two sequences that you can identify in the figure below.
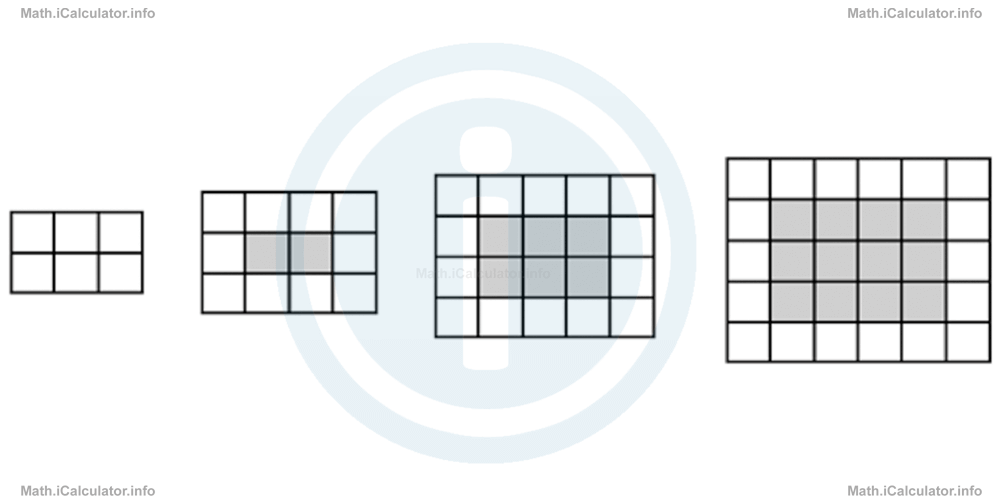
2. Find the number of white and grey squares in the 7th pattern.

Solution 5

1. The shapes in the figure contain two colours: white and grey. The total number of squares for each of the colours forms sequences. Thus,
   1. Total number of white squares sequence = 6, 10, 14, 18. It is an arithmetic sequence where the common difference is d = 4.
   2. Total number of grey squares sequence = 0, 2, 6, 12. It is a quadratic sequence, as the difference between two consecutive terms increases by 2 when moving from left to right.
2. Continuing the sequences for other three terms (to obtain the 7th terms of the above sequences) yields
   1. Total number of white squares sequence = 6, 10, 14, 18, 22, 26, 30
   2. Total number of grey squares sequence = 0, 2, 6, 12, 20, 30, 42

Therefore, if we had a seven^th pattern shown in the figure, it would contain 30 white and 42 grey squares.

More Working with Term-to-Term Rules in Sequences Lessons and Learning Resources

Whats next?

Enjoy the "The Different Types of Sequences Explained" math lesson? People who liked the "Working with Term-to-Term Rules in Sequences lesson found the following resources useful:

1. Types Of Sequences Feedback. Helps other - Leave a rating for this types of sequences (see below)
2. Sequences and Series Math tutorial: Working with Term-to-Term Rules in Sequences. Read the Working with Term-to-Term Rules in Sequences math tutorial and build your math knowledge of Sequences and Series
3. Sequences and Series Video tutorial: Working with Term-to-Term Rules in Sequences. Watch or listen to the Working with Term-to-Term Rules in Sequences video tutorial, a useful way to help you revise when travelling to and from school/college
4. Sequences and Series Revision Notes: Working with Term-to-Term Rules in Sequences. Print the notes so you can revise the key points covered in the math tutorial for Working with Term-to-Term Rules in Sequences
5. Sequences and Series Practice Questions: Working with Term-to-Term Rules in Sequences. Test and improve your knowledge of Working with Term-to-Term Rules in Sequences with example questins and answers
6. Check your calculations for Sequences and Series questions with our excellent Sequences and Series calculators which contain full equations and calculations clearly displayed line by line. See the Sequences and Series Calculators by iCalculator™ below.
7. Continuing learning sequences and series - read our next math tutorial: Working with Arithmetic and Geometric Series. How to find the Sum of the First n-Terms of a Series.

Help others Learning Math just like you

Please provide a rating, it takes seconds and helps us to keep this resource free for all to use

We hope you found this Math tutorial "Working with Term-to-Term Rules in Sequences" useful. If you did it would be great if you could spare the time to rate this math tutorial (simply click on the number of stars that match your assessment of this math learning aide) and/or share on social media, this helps us identify popular tutorials and calculators and expand our free learning resources to support our users around the world have free access to expand their knowledge of math and other disciplines.

Sequences and Series Calculators by iCalculator™

• Arithmetic Progression First Term Calculator
• Arithmetic Progression Two Terms Calculator
• Geometric Progression First Term Calculator
• Geometric Progression Two Terms Calculator
• Binomial Coefficients Calculator
• Infinite Geometric Series Calculator