Menu
Math Lesson 15.7.2 - Transforming Graphs using the Parent Function Graph: Translations
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
Welcome to our Math lesson on Transforming Graphs using the Parent Function Graph: Translations, this is the second lesson of our suite of math lessons covering the topic of Transforming Graphs, you can find links to the other lessons within this tutorial and access additional Math learning resources below this lesson.
Transforming Graphs using the Parent Function Graph: Translations
A translation in mathematics is an action that allows carrying an object (shape, graph, figure, etc.) across the coordinate plane, keeping its size, direction and shape unchanged. The orientation and area of the original mathematical object remain unchanged after a translation as well. Simply put, a translation in math is a vertical shift, horizontal shift, or a combination of the two. Below, we will deal with these two types of translations. Despite - as stated above - translation regards many mathematical objects, our focus in this tutorial will be on graphs' translations only.
The key feature of translations is that it involves only displacements of a graph from the original position but no changes in size or orientation. Let's have a closer look at this important feature.
Horizontal Translations
The first type of translation discussed in this tutorial is horizontal translation. In other words, in this section, we will see how a graph can shift due left or right to the original position. For a better understanding, we will think of this situation as having two identical functions but in different places, not as a single function that moves some units left or right. This is because here we cannot provide animations where the horizontal displacement of a graph is shown dynamically.
The following rules are applied in horizontal translations of graphs.
- A horizontal translation by a units to the right of the graph of a function f(x) is described mathematically by f(x - m).
- A horizontal translation by a units to the left of the graph of a function f(x) is described mathematically by f(x + m).
For example, if we want to displace the parent quadratic function by 3 units on the right (a = 3), we write
f(x - 3) = (x - 3)2
(We are anticipating what is going to be explained in the next chapter, that in f(x - m) functions we can replace the variable x of the original function with x - m and then do the operations.)
In the specific case, we have
= (x - 3)2
= x2 - 6x + 9
Therefore, based on the above rule, we conclude that the graph of the function y = x2 - 6x + 9 is obtained by displacing the graph of y = x2 by three units due right. Let's check whether this conclusion is true by plotting the two graphs in the same coordinate system. Look at the figure below.
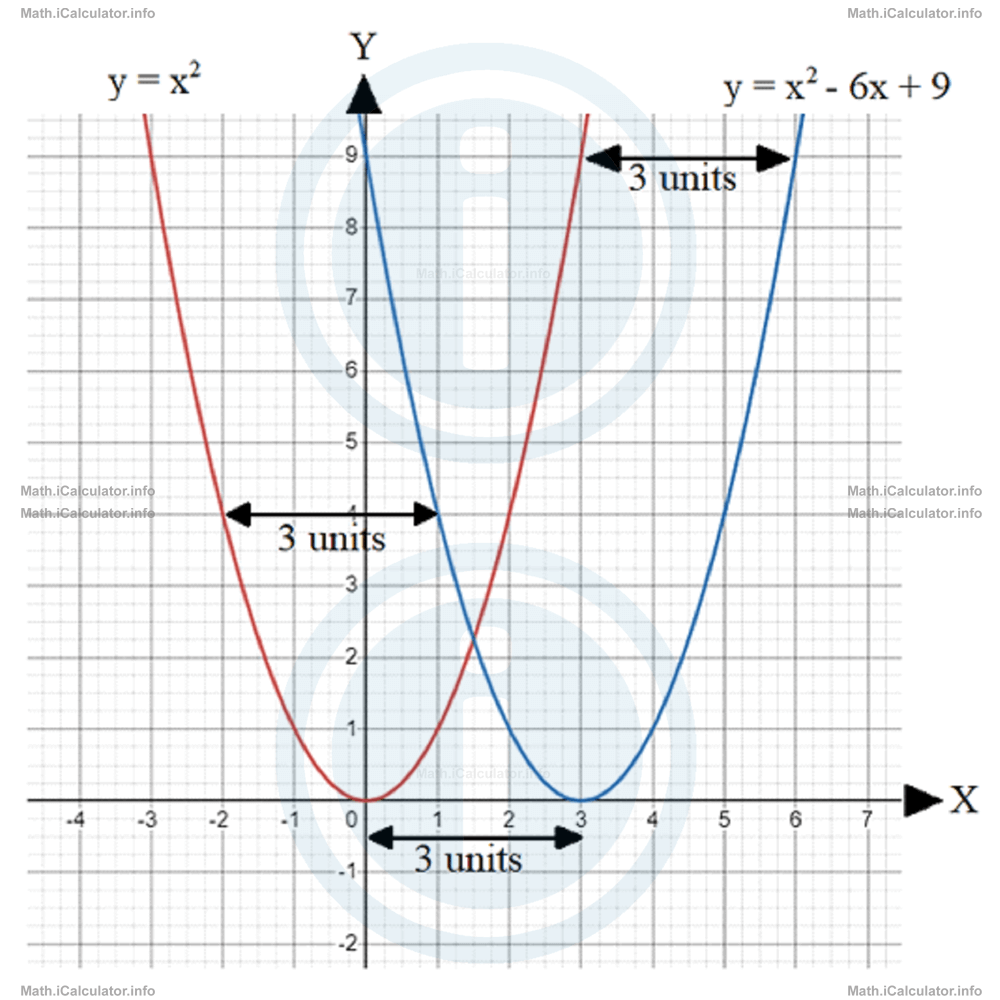
As you see, at every point the two graphs are three units away from each other in the horizontal direction. More precisely, the y = x2 - 3x + 9 graph [which corresponds to y - (x - 3)2 function] is 3 units on the right of the parent function y = x2.
Remark! Recall that f(x) and y represent the same thing in function terminology.
Example 2
Find the formulas of the two functions aside from the function shown in the graph below. Write them in expanded form.
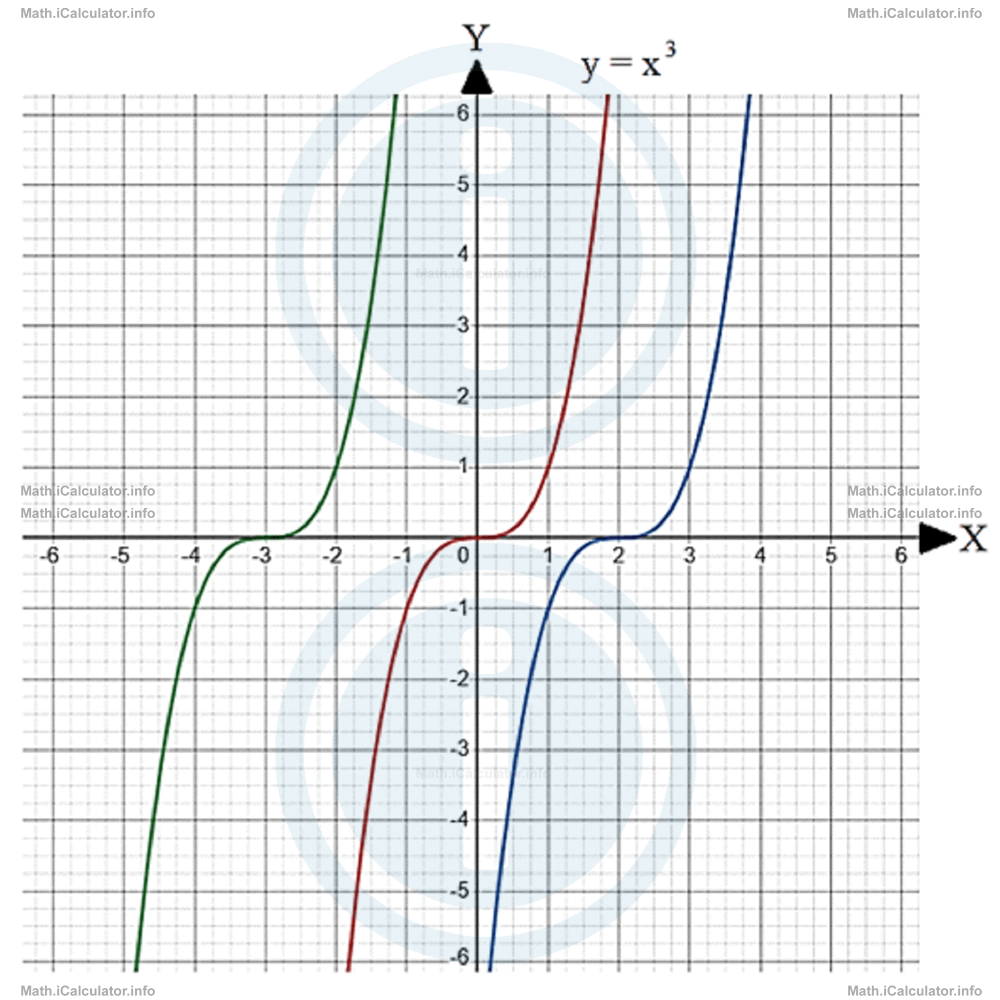
Solution 2
From the figure, it is easy to see that all three graphs are similar. Since the middle graph represents the parent cubic function, the other two graphs represent cubic functions as well.
You can see that the left graph is obtained by displacing the parent graph by 3 units on the left. Hence, the displacement constant is m = -3. The corresponding function therefore is
= [x - (-3)]3
= (x + 3)3
= x3 + 3x2 ∙ 3 + 3 ∙ x ∙ 32 + 33
= x3 + 9x2 + 27x + 27
As for the graph on the right, it is easy to see that it is displaced by 2 units on the right of the parent graph y = x3. Therefore, the displacement constant is m = 2. The corresponding function therefore is
= (x - 2)3
= x3 - 3x2 ∙ 2 + 3x ∙ 22 + 23
= x3 - 6x2 + 12x + 8
Vertical Translations
The second type of translation discussed in this tutorial is vertical translation. In other words, in this section, we will see how a graph can shift due up or down with respect to the original position.
The following rules are applied in horizontal translations of graphs.
- A vertical translation by n units up of the graph of a function f(x) is described mathematically by f(x) + n.
- A vertical translation by c units down of the graph of a function f(x) is described mathematically by f(x) - n.
We have seen the above rules applied in several previous tutorials when finding the y-intercept of various graphs. For example, if we are asked to displace the graph of the function y = 2x by 3 units up (n = 3), we obtain the graph of the function y = 2x + 3, which belongs to the same family as y = 2x but it is 3 units above it, as shown in the figure below.
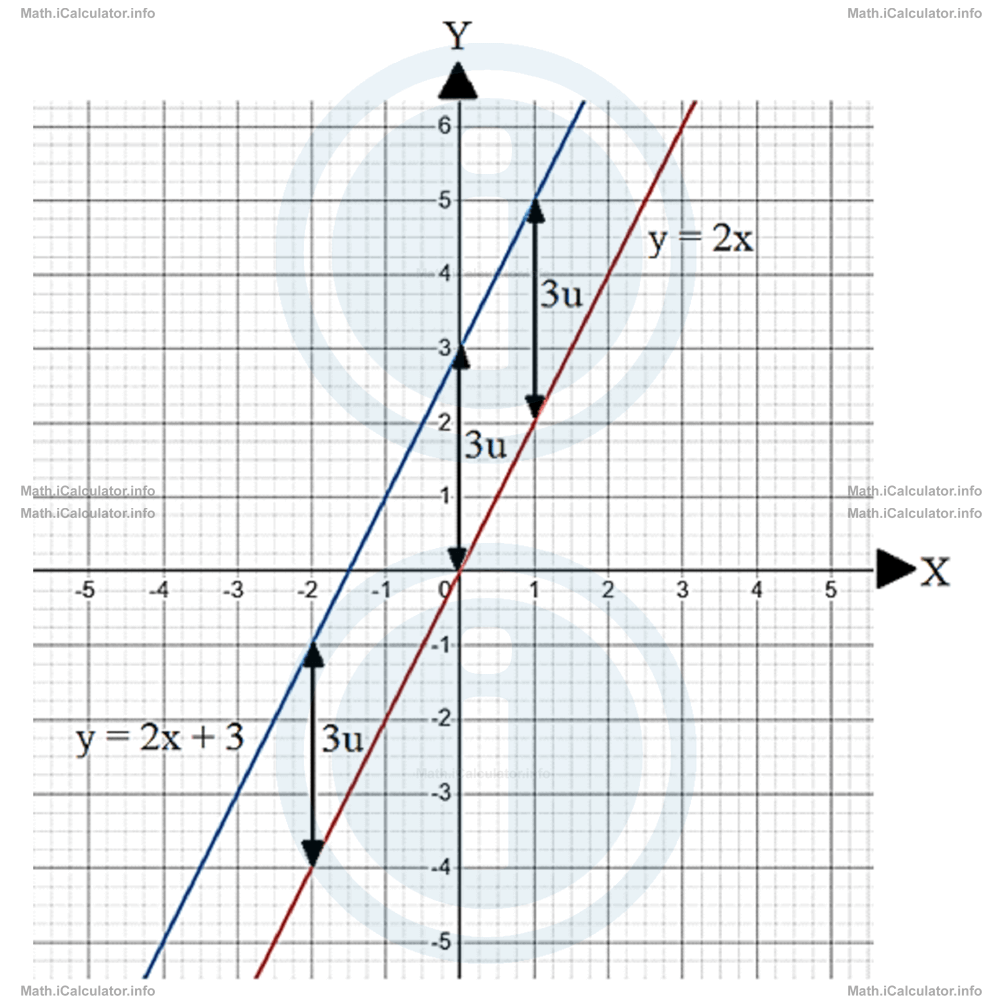
As you see, at every point the y = 2x + 3 graph is 3 units (3u) above the y = 2x graph, given that n = 3.
Remark! Sometimes, the figure is deceiving in the fact that in some parts the graph looks closer to the original than in other parts after a horizontal or a vertical translation. This may lead to the wrong conclusion that the two graphs are not of the same family of functions. If you cannot identify any intersection between the graphs, then it is sure that they belong to the same family of functions. However, the graphs may cross each other and still be of the same family; everything depends on their shape. Let's see the example below for illustration.
Example 3
The figure below shows one known and two unknown graphs. Find the formulas of the unknown graphs.
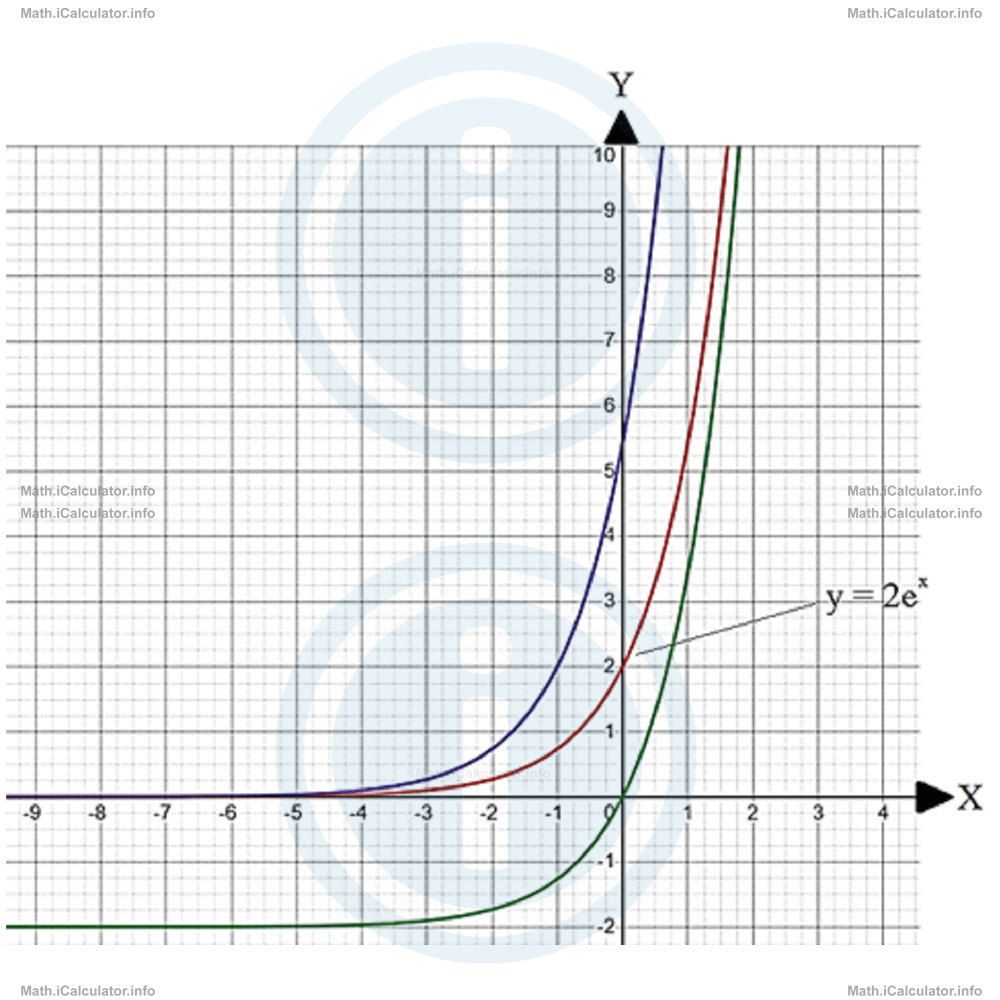
Solution 3
The shape of the three graphs looks similar. Moreover, they do not cross each other. This is an extra argument that all three graphs belong to the same family of functions, i.e. exponential ones given that it is already known that the middle graph is exponential.
It is easy to see (especially in the upper part of the figure) that the purple graph is one unit on the left of the y = 2ex graph. This means we are in the conditions of a horizontal translation of the middle graph by one unit due left based on the general rule f(x) → f(x + m) where m = 1. Hence, since the middle graph represents the function f(x) = y = 2ex, we have for the purple graph,
= 2(ex · e1)
= 2e · ex
Since e ≈ 2.718, we obtain the following formula for the leftmost graph:
Likewise, we can easily see that the green color graph is displaced by 2 units below the y = 2ex graph. Therefore, in this case, we are in the conditions of f(x) + c translation of the middle (known) graph where n = -2. Hence, the formula of the green graph is
The above methods of translation are very useful especially when dealing with quadratic functions of the form y = x2 + bx + c. Please observe the leading coefficient a, which here is 1. We will see later what happens when this coefficient is different from 1. Thus, assuming that we already know some of the points of the y = x2 graph (most people at this stage know how to find the square of the first integers around zero - both positive and negative), we can plot the graph of y = x2 + bx + c by first writing them in the form
Then, we can make a translation of the (known) y = x2 graph by m units horizontally and n units vertically to plot the graph of the above quadratic function.
Example 4
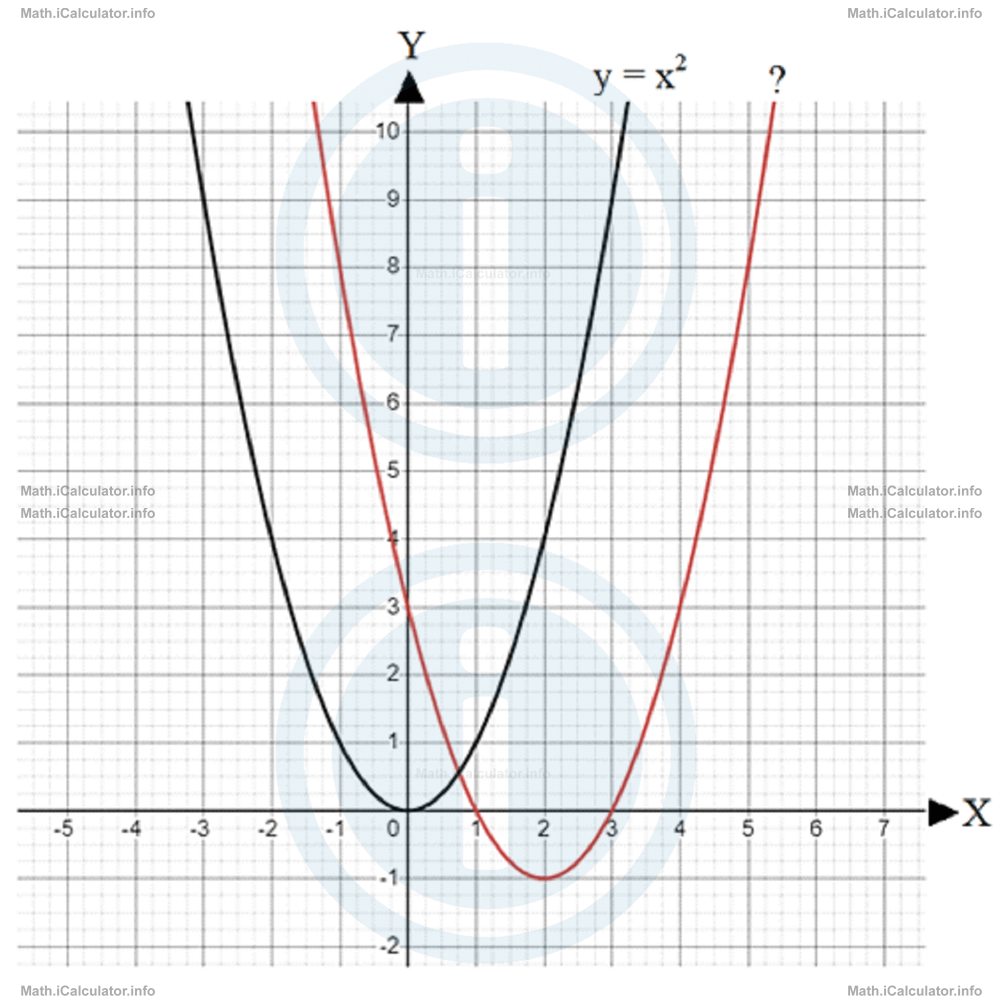
Find the formula of the unknown graph shown in the figure.
Solution 4
By a quick look at the lateral sides of the two graphs it is easy to observe that they keep having the same distance from each other, so the two graphs are of the same family (both are quadratic). Moreover, both graphs have the same dimensions in the sense that one of the graphs is not obtained by any stretching or compression of the other but we have simply some kind of translations involved.
From the figure, we can see that the unknown graph is obtained by translating the y = x2 graph by 2 units on the right and 1 unit down. Therefore, we have m = 2 and n = -1. Therefore, we write the formula of the unknown graph as
= (x - 2)2 - 1
= x2 - 4x + 4 - 1
= x2 - 4x + 3
When the coefficient a of a quadratic function is different from 1, we can factorize it and express the function in the form y = a(x2 + bx/a + c/a). Again, the translation rules are applied for the part of the expression in brackets, and then the values obtained are multiplied by a if necessary. The following example will clarify this point.
Example 5
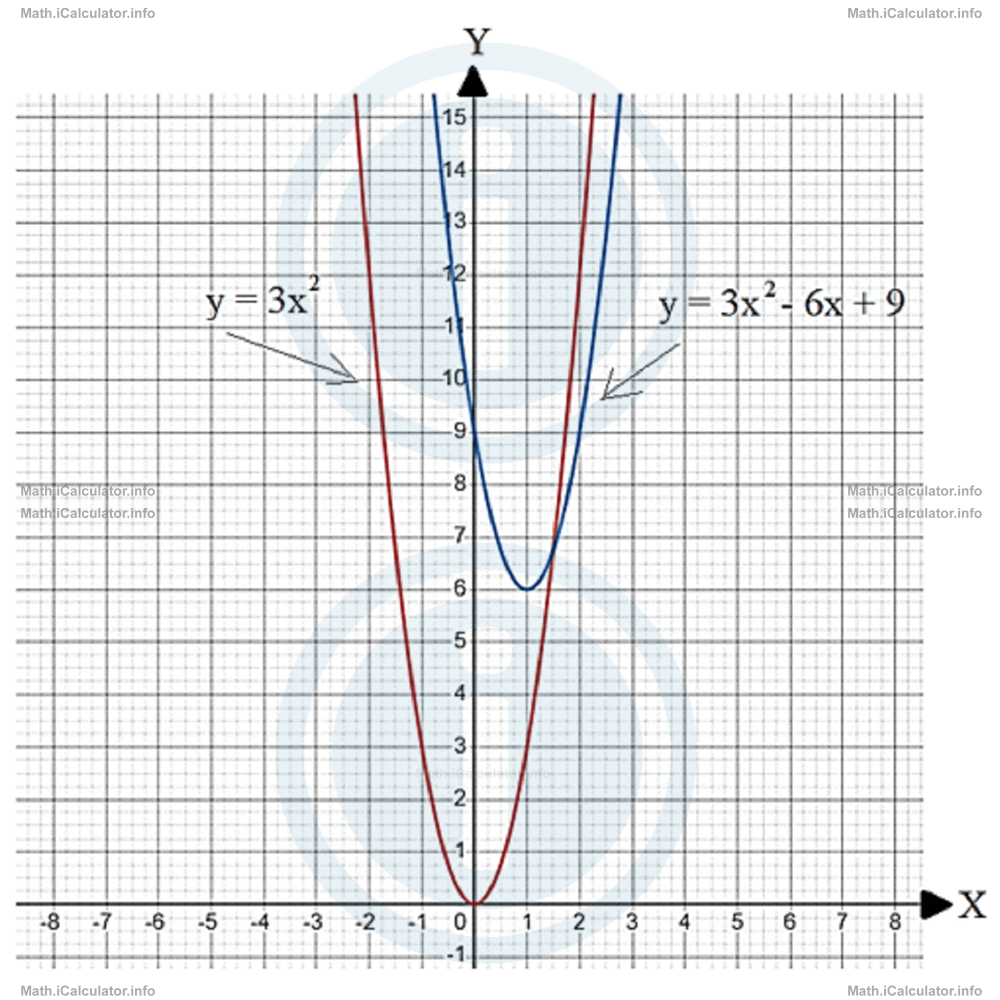
Describe the translations made to plot the graph of the quadratic function y = 3x2 - 6x + 9.
Solution 5
We can write
= 3(x2 - 2x + 3)
= 3(x2 - 2x + 1 + 2)
= 3[(x - 1)2 + 2]
= 3(x - 1)2 + 6
This means the graph of the function y = 3x2 - 6x + 9 is obtained by the translation of the y = 3x graph by one unit due right and 6 units upwards. This result is confirmed by the figure below.
Remark! If there is more than one basic translation to do in a graph, we do it one at a time, not simultaneously. For example, first, we can do the horizontal translation, then the vertical one. The reverse action is also valid.
You have reached the end of Math lesson 15.7.2 Transforming Graphs using the Parent Function Graph: Translations. There are 3 lessons in this physics tutorial covering Transforming Graphs, you can access all the lessons from this tutorial below.
More Transforming Graphs Lessons and Learning Resources
Whats next?
Enjoy the "Transforming Graphs using the Parent Function Graph: Translations" math lesson? People who liked the "Transforming Graphs lesson found the following resources useful:
- Translations Feedback. Helps other - Leave a rating for this translations (see below)
- Types of Graphs Math tutorial: Transforming Graphs. Read the Transforming Graphs math tutorial and build your math knowledge of Types of Graphs
- Types of Graphs Revision Notes: Transforming Graphs. Print the notes so you can revise the key points covered in the math tutorial for Transforming Graphs
- Types of Graphs Practice Questions: Transforming Graphs. Test and improve your knowledge of Transforming Graphs with example questins and answers
- Check your calculations for Types of Graphs questions with our excellent Types of Graphs calculators which contain full equations and calculations clearly displayed line by line. See the Types of Graphs Calculators by iCalculator™ below.
- Continuing learning types of graphs - read our next math tutorial: Gradient of Curves
Help others Learning Math just like you
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
We hope you found this Math tutorial "Transforming Graphs" useful. If you did it would be great if you could spare the time to rate this math tutorial (simply click on the number of stars that match your assessment of this math learning aide) and/or share on social media, this helps us identify popular tutorials and calculators and expand our free learning resources to support our users around the world have free access to expand their knowledge of math and other disciplines.