Menu
Cone Calculator
A Cone is a three-dimensional geometric shape which tapers to a point from a circular base.
Cones are termed "right circular", which denotes the base is circular and the central axis is at right angles to the base.
| Dimension | Value |
|---|---|
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
About the Cone Shape Calculator
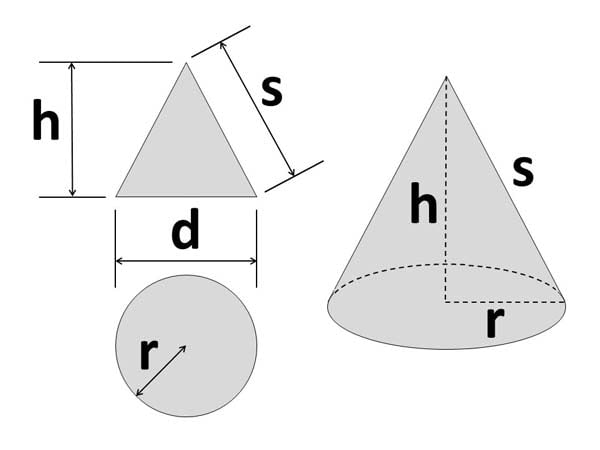
- Height (h): The vertical height of the cone
- Slope Height (s): The length of the sloped side
- Radius (r): Half the diameter of the circular base
- Base Diameter (d): Diameter of the base, equal to twice the radius
- Lateral Surface Area (L): The surface area of the cone in square units excluding the base area
- Base Surface Area (B): Surface area of the circular base in square units
- Total Surface Area (A): Total of the lateral and base surface areas in square units
- Volume: The volume of the cone in cubic units
- You can refine the calculations by controlling the number of decimal places that the calculator calculates to. The default is 2 decimal places.
A cone is a three-dimensional geometric shape that tapers smoothly from a flat base to a point called the apex or vertex. In mathematics, cones are important shapes that have many real-world applications in fields such as architecture, engineering, and physics.
Properties of Cones
Cones have several important properties:
- A cone has a circular base, which is usually denoted as B.
- The height of a cone is the distance from the apex to the center of the base, and is usually denoted as h.
- The slant height of a cone is the distance from the apex to any point on the edge of the base, and is usually denoted as l.
- The lateral surface area of a cone is the area of the curved surface that connects the base to the apex.
- The total surface area of a cone is the sum of the lateral surface area and the area of the base.
- The volume of a cone is the amount of space enclosed by the cone.
Types of Cones
There are two main types of cones:
- Right cones: A cone is a right cone if the apex is directly above the center of the base. In a right cone, the altitude (height) is perpendicular to the base.
- Oblique cones: A cone is an oblique cone if the apex is not directly above the center of the base. In an oblique cone, the altitude (height) is not perpendicular to the base.
Calculating the Volume and Surface Area of Cones
Online calculators make it easy to calculate the volume and surface area of cones. The formulas are:
Volume of a cone: V = (1/3)πr2h
Lateral surface area of a cone: A = πrl
Total surface area of a cone: A = πr(r + l)
where r is the radius of the base, h is the height of the cone, and l is the slant height of the cone.
Understanding cones and their properties is important in math geometry and various fields that utilize three-dimensional shapes. With the help of online calculators, the volume and surface area of cones can be quickly and easily calculated.