Math Lesson 9.4.2 - Applications of Iterative Methods

Please provide a rating, it takes seconds and helps us to keep this resource free for all to use

★★★★★ [ 1 Votes ]

Welcome to our Math lesson on Applications of Iterative Methods, this is the second lesson of our suite of math lessons covering the topic of Iterative Methods for Solving Equations, you can find links to the other lessons within this tutorial and access additional Math learning resources below this lesson.

Applications of Iterative Methods in Geometry

Iterative methods are useful in many fields of science but they are particularly important in geometry, where we often deal with measurements. Thus we often encounter situations, where the quantities measured are irrational because there may be an irrational constant such as Archimedes' constant π involved in the calculations of the area of a circle, the volume of a sphere, etc. Let's explain this point through an example.

Example 3

A sphere was immersed in water and as a result, the volume of water increased by 3140 cm³. Use iterations methods to calculate the radius of this sphere in cm lets assume that your calculator is of a basic type and includes only the four basic operations (addition, subtraction, multiplication and division). Express your answer to one decimal place. Use the formula for calculating the volume of a sphere: V = 4/3 πR³ where π ≈ 3.14.

Solution 3

The volume of the sphere is equal to the volume of the displaced water, as the sphere now occupies the space which was previously occupied by water. Hence, we have V_water = V_sphere = V We have

V = 4/3 πR³

so,

R³ = 3V/4π
= 3 ∙ 3140/4 ∙ 3.14
= 750 cm³

Now, we have to identify an interval that includes the value of the sphere's radius. It is easy to find that this interval extends from 9 cm to 10 cm as (9 cm)3 = 9 cm × 9 cm × 9 cm = 729 cm³ and (10 cm)³ = 10 cm × 10 cm × 10 cm = 1000 cm³. Therefore, it is evident that the radius of our sphere is between 9 cm and 10 cm. Using the half - interval iteration method, we obtain x = 9.5 cm. Thus, since

x³ = 9.5³ = 857.4 cm³

It is clear that the radius is between 9.0 cm and 9.5 cm as 750 is between 729 and 857.4.

Solving again for the half of the new interval, i.e. for x = 9.25 cm, yields

x³ = 9.25³ = 791.5 cm³

This means the radius is between 9.0 cm and 9.25 cm, as 750 is between 729 and 857.4. Hence, taking the new half - interval as x = 9.125 cm, we obtain

x³ = 9.125³ = 759.8 cm³

Therefore, the result is between 9.0 cm and 9.125 cm as 750 is between 729 and 759.8. Hence, since we want to express the result in one decimal place, we write R = 9.1 cm.

Now, let's consider another example about the use of iterative methods in geometry but this time involving the area of figures.

Example 4

A rectangle has an area of 200 cm². One of the sides is 9 cm longer than the other.

Find a suitable equation that gives the rectangle's area in terms of its sides.
Identify the one unit range between two integers where the shortest side takes the value.
Find the lengths of each side expressed in one decimal place.
Estimate the error made when using such methods of approximation by calculating again the area of the rectangle, this time using the dimensions found in (c).

Solution 4

We can denote the smallest side by a letter, for example, x. Therefore, the longest side is x + 9, where both x and x + 9 are expressed in cm. 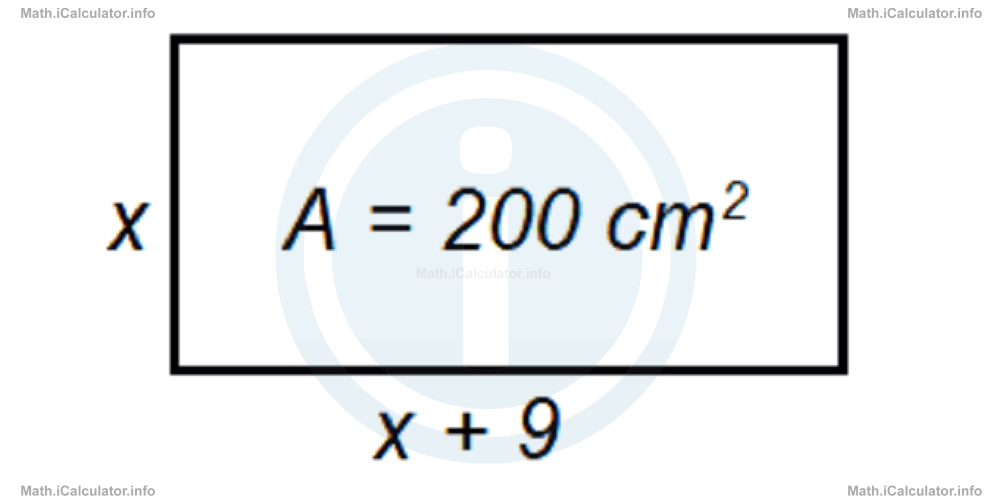$Math Tutorials: Iterative Methods for Solving Equations Example$ Since the area of a rectangle is calculated by multiplying its dimensions, we have the relation
A = x ∙ (x + 9)
for the area of our rectangle. Thus, since A = 200 cm², the equation expressing the sides of this rectangle is
x(x + 9) = 200
x² + 9x = 200
x² + 9x - 200 = 0
This is a quadratic equation that cannot be factorised, as we did in tutorial 6.4. Therefore, we must try other methods to find the value of x.
We make a quick mental calculation to identify the possible range of the two consecutive integers where the value of x may be. Thus, taking x = 10 yields
x² + 9x - 200
= 10² + 9 ∙ 10 - 200
= 100 + 90 - 200
= - 10 (negative)
Hence, 10 is the lower bound of the interval, as explained in tutorial 2.2. The next value, therefore, (the one that represents the upper bound) must be bigger. Taking x = 11 yields
x² + 9x - 200
= 11² + 9 ∙ 11 - 200
= 121 + 99 - 200
= 20 (positive)
Therefore, now we are sure that the smaller side x is greater than 10 and smaller than 11.
Since we are not able to find an exact value for x, it is necessary to use iterative methods to find its approximate value to one decimal place. It is better to use the 'half - interval division' method instead of the 'going through values in order' method, as since we want the result expressed to one decimal place, the half interval method does not require more than 3 - 4 steps in all. Thus, since half interval between 10 and 11 corresponds to 10.5, we have
x² + 9x - 200
= 10.5² + 9 ∙ 10.5 - 200
= 110.25 + 94.5 - 200
= 4.75 (positive)
This means the result is in the lower part of the interval, i.e. between 10 and 10.5. Thus, for x = 10.25 (halfway between 10 and 10.5), we have
x² + 9x - 200
= 10.25² + 9 ∙ 10.25 - 200
= 105.0625 + 92.25 - 200
= - 2.6875 (negative)
Hence, x lies between 10.25 and 10.5 (values that give opposite signs). Taking again halfway between these two values, i.e. x = 10.375, yields
x² + 9x - 200
= 10.375² + 9 ∙ 10.375 - 200
= 107.64 + 93.375 - 200
= 1.015 (positive)
This means the result lies between 10.25 and 10.375. When rounding it to one decimal place, we obtain x = 10.3 cm. In this way, we found the length of the shorter side (width, W).
The value of the longest side (length, L) therefore is x + 9 = 10.3 cm + 9 cm = 19.3 cm.
Now, let's calculate the rectangle's area using the dimensions we just found. Thus,
A = L × W
= 19.3 cm × 10.3 cm
= 198.79 cm²
This value is very close to the original one. The error is only 200 cm² - 198.79 cm² = 1.21 cm². However, this error would be much smaller if we increased the accuracy of dimensions calculation to 2 decimal places or more. This means the result would be much closer to the original value (200 cm²).

More Iterative Methods for Solving Equations Lessons and Learning Resources

Equations Learning Material
Tutorial ID	Math Tutorial Title	Revision Notes	Revision Questions
9.4	Iterative Methods for Solving Equations
Lesson ID	Math Lesson Title	Lesson	Video Lesson
9.4.1	Iterative Methods for Solving Equations
9.4.2	Applications of Iterative Methods
9.4.3	Exercises involving Iteration
9.4.4	Recursive Iteration and Iteration Machines

Whats next?

Enjoy the "Applications of Iterative Methods" math lesson? People who liked the "Iterative Methods for Solving Equations lesson found the following resources useful:

Applications Feedback. Helps other - Leave a rating for this applications (see below)
Equations Math tutorial: Iterative Methods for Solving Equations. Read the Iterative Methods for Solving Equations math tutorial and build your math knowledge of Equations
Equations Video tutorial: Iterative Methods for Solving Equations. Watch or listen to the Iterative Methods for Solving Equations video tutorial, a useful way to help you revise when travelling to and from school/college
Equations Revision Notes: Iterative Methods for Solving Equations. Print the notes so you can revise the key points covered in the math tutorial for Iterative Methods for Solving Equations
Equations Practice Questions: Iterative Methods for Solving Equations. Test and improve your knowledge of Iterative Methods for Solving Equations with example questins and answers
Check your calculations for Equations questions with our excellent Equations calculators which contain full equations and calculations clearly displayed line by line. See the Equations Calculators by iCalculator™ below.
Continuing learning equations - read our next math tutorial: Quadratic Equations

Help others Learning Math just like you