Solving Systems With One Linear And One Quadratic Equation Calculator

Please provide a rating, it takes seconds and helps us to keep this resource free for all to use

The Solving Systems With One Linear And One Quadratic Equation Calculator will calculate:

1. The values of the variables x and y in any system of equations where one is linear and the other quadratic.

Solving Systems With One Linear And One Quadratic Equation Calculator

🖹 Normal View🗖 Full Page View

Calculator Precision (Decimal Places)0123456789101112131415

Coefficient preceding x in the linear equation (a1)

Coefficient preceding y in the linear equation (b1)

Constant of the linear equation (c1)

Coefficient preceding x2 in the quadratic equation (a2)

Coefficient preceding x in the quadratic equation (b2)

Constant of the quadratic equation (c2)

Please note that the formula for each calculation along with detailed calculations is shown further below this page. As you enter the specific factors of each solving systems with one linear and one quadratic equation calculation, the Solving Systems With One Linear And One Quadratic Equation Calculator will automatically calculate the results and update the formula elements with each element of the solving systems with one linear and one quadratic equation calculation. You can then email or print this solving systems with one linear and one quadratic equation calculation as required for later use.

We hope you found the Solving Systems With One Linear And One Quadratic Equation Calculator useful, if you did, we kindly request that you rate this calculator and, if you have time, share to your favourite social network. This allows us to allocate future resource and keep these Math calculators and educational material free for all to use across the globe.

Please provide a rating, it takes seconds and helps us to keep this resource free for all to use

Related Fields with Tutorials

1. Engineering
2. Physics

Theoretical description

A system of equations where one is linear and the other is quadratic has the general form where a1, b1, a2 and b2 are coefficients (the first two belong to the linear equation while the rest belong to the quadratic equation) and c1, c2 are the constants of the two equations of the system. Solving such a system means finding the possible values of x and y which when substituted in the original equations give true results. For example, in the system of equationsthe number pairs (1, 2) and (-4, 7) (which represent the intercepts of the two lines on the graph) are solutions to the system, as when inserted in the place of x and y in the original equations give true results. Indeed, andSince the two equations have not the same degree, the only analytical method available for solving the system is the substitution method. According to this method, the variable y in the linear equation is expressed in terms of the other variable x and then, it is substituted in the quadratic equation. For example, in the system shown above, we can write y = 3 - x for the linear equation and after substituting it into the quadratic equation, this yieldsorwhere a = 1, b = 3 and c = -4. Hence, using the quadratic formula for solving this new quadratic equation for the variable x yieldsandThe corresponding y-values therefore areand In this way, we obtained the two pairs of solutions (-4, 7) and (1, 2) for the given system of equations (as expected). This example corresponds to the cases when the straight line that corresponds to the linear equation graph "pierces" the parabola representing the graph of the quadratic equation, as shown in the figure below. 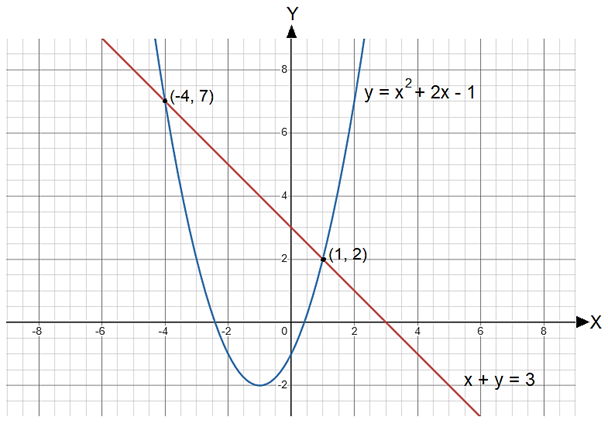Obviously, this cannot happen always; sometimes the linear graph "touches" the parabola at a single point (it is tangent). This occurs when the discriminant of the new quadratic equation obtained after substituting the linear equation into the quadratic one is zero. Moreover, there are cases when the two graphs do not touch each other at all. This occurs when the discriminant of the abovementioned quadratic equation is negative. Obviously, you don't have to follow such a long procedure as the one described above when solving systems with one linear and one quadratic equation, as our calculator solves the system automatically. You only have to insert the coefficients and constants of the two equations and the result will be displayed automatically. Thus, after making a series of substitutions and transformations in the system derived from the fact that the variable y is expressed in terms of x in the quadratic equation, yields the four formulas below, that give the two possible pairs of solutions (sometimes they show the message "no solution", or the solutions may be equal, depending on the sign of the discriminant).