Menu
Identifying Factors Number Calculator
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
The Identifying Factors Number Calculator will calculate:
- All factors (both prime and non prime) of a given number.
Identifying Factors Number Calculator Parameters: All numbers entered must be whole
| Identifying Factors Number Calculator Input Values |
|---|
| Number (N) = |
Please note that the formula for each calculation along with detailed calculations is shown further below this page. As you enter the specific factors of each identifying factors number calculation, the Identifying Factors Number Calculator will automatically calculate the results and update the formula elements with each element of the identifying factors number calculation. You can then email or print this identifying factors number calculation as required for later use.
We hope you found the Identifying Factors Number Calculator useful, if you did, we kindly request that you rate this calculator and, if you have time, share to your favourite social network. This allows us to allocate future resource and keep these Math calculators and educational material free for all to use across the globe.
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
Theoretical description
By definition, a factor is a number that divides another (bigger) number. For example, 4 is a factor of 12 because 4 divides 12. Another name used for factor is divisor.
Factors are very important in practice as they tell us all possible divisions we can apply to a whole. For example, if we have 48 kg of fruits, we can use various ways to pack them in equal boxes by identifying all factors of 48. Thus, in these conditions we can prepare:
24 boxes of 2 kg each as 24 × 2 kg = 48 kg
16 boxes of 3 kg each as 16 × 3 kg = 48 kg
12 boxes of 4 kg each as 12 × 4 kg = 48 kg
8 boxes of 6 kg each as 8 × 6 kg = 48 kg
6 boxes of 8 kg each as 6 × 8 kg = 48 kg
4 boxes of 12 kg each as 4 × 12 kg = 48 kg
3 boxes of 16 kg each as 3 × 16 kg = 48 kg
2 boxes of 24 kg each as 2 × 24 kg = 48 kg
1 box of 48 kg as 1 × 48 kg = 48 kg
There is a method known as the "tree method" used to identify the prime factors of a number, as shown in the figure below. 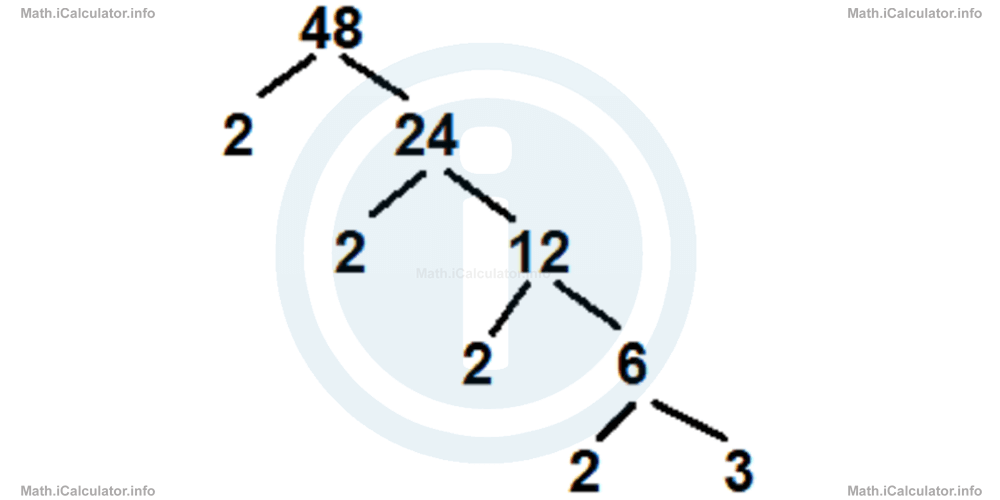
Thus, based on the tree method described in the figure, 48 can be written as a product of prime factors, i.e. 48 = 2 × 2 × 2 × 2 × 3 = 24 × 3. However, by combining (multiplying) two or more prime factors we can also find the other (composite) factors of the given number. Thus, in our example we have 2 × 2 = 4; 2 × 3 = 6; 2 × 2 × 2 = 8; 2 × 2 × 3 = 12; 2 × 2 × 2 × 2 = 16; 2 × 2 × 2 × 3 = 24 and 2 × 2 × 2 × 2 × 3 = 48. Also, another factor of a given number is the number itself (here 48).
In this calculator, you will insert a number as the input and the calculator will calculate and display all factors (prime and composite) of that number as output. This will save you precious time in identifying all factors of a number, especially when that number is big.
Arithmetic Math Tutorials associated with the Identifying Factors Number Calculator
The following Math tutorials are provided within the Arithmetic section of our Free Math Tutorials. Each Arithmetic tutorial includes detailed Arithmetic formula and example of how to calculate and resolve specific Arithmetic questions and problems. At the end of each Arithmetic tutorial you will find Arithmetic revision questions with a hidden answer that reveal when clicked. This allows you to learn about Arithmetic and test your knowledge of Math by answering the revision questions on Arithmetic.
- 1.1 - Numbering Systems, a Historical View
- 1.2 - Number Sets, Positive and Negative Numbers and Number Lines
- 1.3 - Operations with Numbers and Properties of Operations
- 1.4 - Order of Operations and PEMDAS Rule
- 1.5 - Multiples, Factors, Prime Numbers and Prime Factorization including LCM and GCF
- 1.6 - Divisibility Rules
- 1.7 - Decimal Number System and Other Numbering Systems