Menu
Regular Polgon Calculator
Use this online math calculator to calculate the properties of a regular polygon.
A Polygon is a two-dimensional shape with straight sides and no gap
A Regular Polygon has equal sides (the angle calculations are based on a regular polygon)
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
About the Regular Polygon Calculator
The regular polygon calculator gives you all the required information about a regular polygon depending upon the number of sides it has. In this article, we will discuss the basics of polygons We will talk about what a polygon is, different types of polygons and see why a regular polygon calculator is needed in daily life.
So, let's begin with the basics
What is a Regular Polygon?
A polygon is a closed 2 dimensional geometric figure consisting of at least 3 lines. However, not every polygon is a regular polygon. A regular polygon is equilateral and equiangular.
- Equilateral: All sides equalv
- Equiangular: All angles equal
And thus, an equilateral triangle, a square, and such shapes are regular polygons.
Properties of a Regular Polygon
Apart from the aforementioned fact that a regular polygon has equal sides and angles, it also possesses the following properties:
- Interior angle bisectors meet at the center of the polygon.
- Lines drawn from the center of the polygon to each vertex are equal in length.
- The center of the polygon is also the center to all the inscribed and circumscribed circles drawn on the polygon.
- The formula to calculate the angle of a regular polygon with n number of sides is [(2n-4)/n] x 90°.
- Straight lines drawn from the center to each vertex also create as many isosceles triangles as the number of sides of the polygon.
Types of Regular Polygons
While there can be any number of sides of a polygon, let's take a look at the most common regular polygons:
- 3 sides: a trigon (triangle)
- 4 sides: a tetragon or a quadrilateral
- 5 sides: pentagon
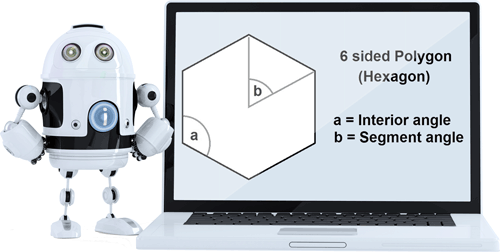
- 6 sides: hexagon
- 7 sides: heptagon
- 8 sides: octagon
- 9 sides: nonagon
- 10 sides: decagon
Common Formulas of a Regular Polygon
A regular polygon, like any other geometrical figure, has certain formulas to calculate its area, perimeter and other values. Let there be a regular polygon with 'n' number of sides and a side length 'a'. thus,
- Area of a Regular Polygon: n x a² x cot (π/n)/4
- Perimeter: n x a
- Interior angle: (n-2) x π/n
- Exterior angle: 180°- interior angle or 2 x π/n
How the Regular Polygon Calculator Works
The regular polygon calculator is an extremely easy to use web application that requires you to simply type in number of sides. The calculator will then calculate the interior angle, the segment angle and also tell the name of the polygon automatically.
Use of Regular Polygons in Daily Life
Polygons revolve around a lot of things in our life. Most of the daily things we use are built around the varying shapes of polygons. Floor tiles are polygons, stop signs are octagons, so are honeycombs. At the same time, building are quadrilaterals. The spokes of a wheel are installed using a complex polynomial structure that many of us are unaware of.
The stars you hang on the Christmas Tree are made in the shape of a pentagram; the five pointed star creates a perfect pentagon. In the case of simple machines, a nut is hexagonal from the outside. A boxing ring is a tetragon a square. At the same time, MMA (mixed martial arts) ring, especially that of UFC is an octagon, and that's how they address it. Many trampolines come in various sizes of hexagons or octagons too.
The construction cost is calculated by segregating a building into smaller polygons. For example, a sliding roof is a triangle and thus has different area. Talk to any tile installer and you'll see how they are able to calculate the number of hexagonal tiles fixed perfectly in a rectangular room. They are all around us, we simply need to observe what we see.