Math Lesson 12.3.5 - The Binomial Coefficients Theorem

Please provide a rating, it takes seconds and helps us to keep this resource free for all to use

★★★★★ [ 3 Votes ]

Welcome to our Math lesson on The Binomial Coefficients Theorem , this is the fifth lesson of our suite of math lessons covering the topic of Binomial Expansion and Coefficients, you can find links to the other lessons within this tutorial and access additional Math learning resources below this lesson.

The Binomial Coefficients Theorem Explained

This theorem, first discovered by Sir Isaac Newton, says that the coefficients preceding the variables in binomials raised to a given power are as follows:

(a + b)ⁿ = (n/0) ∙ aⁿ ∙ b⁰ + (n/1) ∙ a^{n - 1} ∙ b¹ + (n/2) ∙ a^{n - 2} ∙ b² + ⋯ + (n/k) ∙ a^{n - k} ∙ b^k + ⋯ + (n/n - 1) ∙ a¹ ∙ b^{n - 1} + (n/n) ∙ a⁰ ∙ bⁿ

The general term of this binomial expression therefore is

(n/k) a^{n - k} b^k

Hence, the algebraic form of expansion of the binomial expression (a + b)ⁿ is

(a + b)ⁿ = ⁿ∑_{k = 0}(n/k) a^{n - k} b^k

where the symbol "ⁿ∑_{k = 0}" is an abbreviation that means "the sum of all terms from k = 0 to k = n".

From the above formula and from the definition of factorial, it is clear that the first and the last coefficients are both 1, because

(n/0) = C(n,0) = n!/0!(n - 0)! = n!/1 ∙ n! = 1

and

(n/n) = C(n,n) = n!/n!(n - n)! = n!/(n! ∙ 0!) = n!/(n! ∙ 1) = 1

We observed this fact in all examples discussed so far, where the leading and the trailing coefficients were both 1.

Let's prove the formula of the binomial coefficients by calculating them through the above method and eventually comparing the results obtained by all values shown in the Pascal's Triangle Table.

For n = 0, we have:

(a + b)⁰ = (0/0) ∙ a⁰ ∙ b⁰
= 1 ∙ 1
= 1

For n = 2, we have

(a + b)¹ = (1/0) ∙ a¹ ∙ b⁰ + (1/1) ∙ a^{1 - 1} ∙ b¹
= 1 ∙ a ∙ 1 + 1!/1!(1-1)! ∙ a⁰ ∙ b
= a + b

For n = 2, we have

(a + b)² = (2/0) ∙ a² ∙ b⁰ + (2/1) ∙ a^{2 - 1} ∙ b¹ + (2/2) ∙ a^{2 - 2} ∙ b²
= 2!/0!(2 - 0)! ∙ a² ∙ b⁰ + 2!/1!(2 - 1)! ∙ a¹ ∙ b¹ + 2!/2!(2 - 2)! ∙ a⁰ ∙ b²
= 2!/1 ∙ 2! ∙ a² ∙ 1 + 2!/1! ∙ 1! ∙ a¹ ∙ b¹ + 2!/2! ∙ 0! ∙ 1 ∙ b²
= 1 ∙ a² ∙ 1 + 2 ∙ 1/1 ∙ 1 ∙ a¹ ∙ b¹ + 1 ∙ 1 ∙ b²
= a² + 2ab + b²

For n = 3, we have

(a + b)³ = (3/0) ∙ a³ ∙ b⁰ + (3/1) ∙ a^{3 - 1} ∙ b¹ + (3/2) ∙ a^{3 - 2} ∙ b² + (3/3) ∙ a^{3 - 3} ∙ b³
= 3!/0!(3 - 0)! ∙ a³ ∙ b⁰ + 3!/1!(3 - 1)! ∙ a² ∙ b¹ + 3!/2!(3 - 2)! ∙ a¹ ∙ b² + 3!/3!(3 - 3)! ∙ a⁰ ∙ b³
= 3!/1! ∙ 3! ∙ a³ + 3!/1! ∙ 2! ∙ a² b + 3!/2! ∙ 1! ∙ ab² + 3!/3! ∙ 0! ∙ b³
= a³ + 3a² b + 3ab² + b³

For n = 4, we have

(a + b)⁴ = (4/0) ∙ a⁴ ∙ b⁰ + (4/1) ∙ a^{4 - 1} ∙ b¹ + (4/2) ∙ a^{4 - 2} ∙ b² + (4/3) ∙ a^{4 - 3} ∙ b³ + (4/4) ∙ a^{4 - 4} ∙ b⁴
= 4!/0!(4 - 0)! ∙ a⁴ ∙ b⁰ + 4!/1!(4 - 1)! ∙ a³ ∙ b¹ + 4!/2!(4 - 2)! ∙ a² ∙ b² + 4!/3!(4 - 3)! ∙ a¹ ∙ b³ + 4!/4!(4 - 4)! ∙ a⁰ ∙ b⁴
= 4!/1 ∙ 4! ∙ a⁴ + 4!/1! ∙ 3! ∙ a³ ∙ b + 4!/2! ∙ 2! ∙ a² ∙ b² + 4!/3! ∙ 1! ∙ a ∙ b³ + 4!/4! ∙ 0! ∙ b⁴
= a⁴ + 4a³ b + 4 ∙ 3 ∙ 2 ∙ 1/2 ∙ 1 ∙ 2 ∙ 1 a² b² + 4ab³ + b⁴
= a⁴ + 4a³ b + 6a² b² + 4ab³ + b⁴

For n = 5, we have

(a + b)⁵ = (5/0) ∙ a⁵ ∙ b⁰ + (5/1) ∙ a^{5 - 1} ∙ b¹ + (5/2) ∙ a^{5 - 2} ∙ b² + (5/3) ∙ a^{5 - 3} ∙ b³ + (5/4) ∙ a^{5 - 4} ∙ b⁴ + (5/5) ∙ a^{5 - 5} ∙ b⁵
= 5!/0!(5 - 0)! ∙ a⁵ ∙ b⁰ + 5!/1!(5 - 1)! ∙ a⁴ ∙ b¹ + 5!/2!(5 - 2)! ∙ a³ ∙ b² + 5!/3!(5 - 3)! ∙ a² ∙ b³ + 5!/4!(5 - 4)! ∙ a¹ ∙ b⁴ + 5!/5!(5 - 5)! ∙ a⁰ ∙ b⁵
= 5!/1! ∙ 5! ∙ a⁵ + 5!/1! ∙ 4! ∙ a⁴ ∙ b + 5!/2! ∙ 3! ∙ a³ ∙ b² + 5!/3! ∙ 2! ∙ a² ∙ b³ + 5!/4! ∙ 1! ∙ a ∙ b⁴ + 5!/5! ∙ 0! ∙ b⁵
= a⁵ + 5 ∙ 4!/1 ∙ 4! a⁴ b + 5 ∙ 4 ∙ 3!/2 ∙ 1 ∙ 3! a³ b² + 5 ∙ 4 ∙ 3!/3! ∙ 2 ∙ 1 a² b³ + 5 ∙ 4!/4! ∙ 1 ab⁴ + 5!/5! ∙ 1 b⁵
= a⁵ + 5a⁴ b + 10a³ b² + 10a² b³ + 5ab⁴ + b⁵

For n = 6, we have

(a + b)⁶ = (6/0) ∙ a⁶ ∙ b⁰ + (6/1) ∙ a^{6 - 1} ∙ b¹ + (6/2) ∙ a^{6 - 2} ∙ b² + (6/3) ∙ a^{6 - 3} ∙ b³ + (6/4) ∙ a^{6 - 4} ∙ b⁴ + (6/5) ∙ a^{6 - 5} ∙ b⁵ + (6/6) ∙ a^{6 - 6} ∙ b⁶
= 6!/0!(6 - 0)! ∙ a⁶ ∙ b⁰ + 6!/1!(6 - 1)! ∙ a⁵ ∙ b¹ + 6!/2!(6 - 2)! ∙ a⁴ ∙ b² + 6!/3!(6 - 3)! ∙ a³ ∙ b³ + 6!/4!(6 - 4)! ∙ a² ∙ b⁴ + 6!/5!(6 - 5)! ∙ a¹ ∙ b⁵ + 6!/6!(6 - 6)! ∙ a⁰ ∙ b⁶
= 6!/0! ∙ 6! ∙ a⁶ ∙ b⁰ + 6!/1! ∙ 5! ∙ a⁵ ∙ b¹ + 6!/2! ∙ 4! ∙ a⁴ ∙ b² + 6!/3! ∙ 3! ∙ a³ ∙ b³ + 6!/4! ∙ 2! ∙ a² ∙ b⁴ + 6!/5! ∙ 1! ∙ a¹ ∙ b⁵ + 6!/6! ∙ 0! ∙ a⁰ ∙ b⁶
= 6!/(1 ∙ 6! ∙ a⁶ ∙ 1 + 6 ∙ 5!/1 ∙ 5! ∙ a⁵ ∙ b + 6 ∙ 5 ∙ 4!/2 ∙ 1 ∙ 4! ∙ a⁴ ∙ b² + 6 ∙ 5 ∙ 4 ∙ 3!/3 ∙ 2 ∙ 1 ∙ 3! ∙ a³ ∙ b³ + 6 ∙ 5 ∙ 4!/4! ∙ 2 ∙ 1 ∙ a² ∙ b⁴ + 6 ∙ 5!/5! ∙ 1 ∙ a¹ ∙ b⁵ + 6!/6! ∙ 1 ∙ 1 ∙ b⁶
= a⁶ + 6a⁵ b + 15a⁴ b² + 20a³ b³ + 15a² b⁴ + 6ab⁵ + b⁶

For n = 7, we have

(a + b)⁷ = (7/0) ∙ a⁷ ∙ b⁰ + (7/1) ∙ a^{7 - 1} ∙ b¹ + (7/2) ∙ a^{7 - 2} ∙ b² + (7/3) ∙ a^{7 - 3} ∙ b³ + (7/4) ∙ a^{7 - 4} ∙ b⁴ + (7/5) ∙ a^{7 - 5} ∙ b⁵ + (7/6) ∙ a^{7 - 6} ∙ b⁶ + (7/7) ∙ a^{7 - 7} ∙ b⁷
= 7!/0!(7 - 0)! ∙ a⁷ ∙ b⁰ + 7!/1!(7 - 1)! ∙ a⁶ ∙ b¹ + 7!/2!(7 - 2)! ∙ a⁵ ∙ b² + 7!/3!(7 - 3)! ∙ a⁴ ∙ b³ + 7!/4!(7 - 4)! ∙ a³ ∙ b⁴ + 7!/5!(7 - 5)! ∙ a² ∙ b⁵ + 7!/6!(7 - 6)! ∙ a¹ ∙ b⁶ + 7!/7!(7 - 7)! ∙ a⁰ ∙ b⁷
= 7!/0! ∙ 7! ∙ a⁷ ∙ b⁰ + 7!/1! ∙ 6! ∙ a⁶ ∙ b¹ + 7!/2! ∙ 5! ∙ a⁵ ∙ b² + 7!/3! ∙ 4! ∙ a⁴ ∙ b³ + 7!/4! ∙ 3! ∙ a³ ∙ b⁴ + 7!/5! ∙ 2! ∙ a² ∙ b⁵ + 7!/6! ∙ 1! ∙ a¹ ∙ b⁶ + 7!/7! ∙ 0! ∙ a⁰ ∙ b⁷
= 7!/1 ∙ 7! ∙ a⁷ ∙ 1 + 7 ∙ 6!/1! ∙ 6! ∙ a⁶ ∙ b + 7 ∙ 6 ∙ 5!/2 ∙ 1 ∙ 5! ∙ a⁵ ∙ b² + 7 ∙ 6 ∙ 5 ∙ 4!/3 ∙ 2 ∙ 1 ∙ 4! ∙ a⁴ ∙ b³ + 7 ∙ 6 ∙ 5 ∙ 4!/4! ∙ 3 ∙ 2 ∙ 1 ∙ a³ ∙ b⁴ + 7 ∙ 6 ∙ 5!/5! ∙ 2 ∙ 1 ∙ a² ∙ b⁵ + 7 ∙ 6!/6! ∙ 1 ∙ a ∙ b⁶ + 7!/7! ∙ 1 ∙ 1 ∙ b⁷
= a⁷ + 7a⁶ b + 21a⁵ b² + 35a⁴ b³ + 35a³ b⁴ + 21a² b⁵ + 7ab⁶ + b⁷

If you compare all coefficients found above using the Binomial Coefficients Formula with those in the Pascal's Triangle Table, you will find out that they fit perfectly. Therefore, now we have a much more powerful method for calculating the binomial coefficients of any degree.

Example 3

Find all coefficients of the binomial (x + y)¹⁰ when written in the expanded form.

Solution 3

Let's make a table for a better understanding. Since, the number of terms in a binomial is 1 more than its degree, the table will have 11 rows in total, each of them representing a particular term of the binomial in the expanded form.

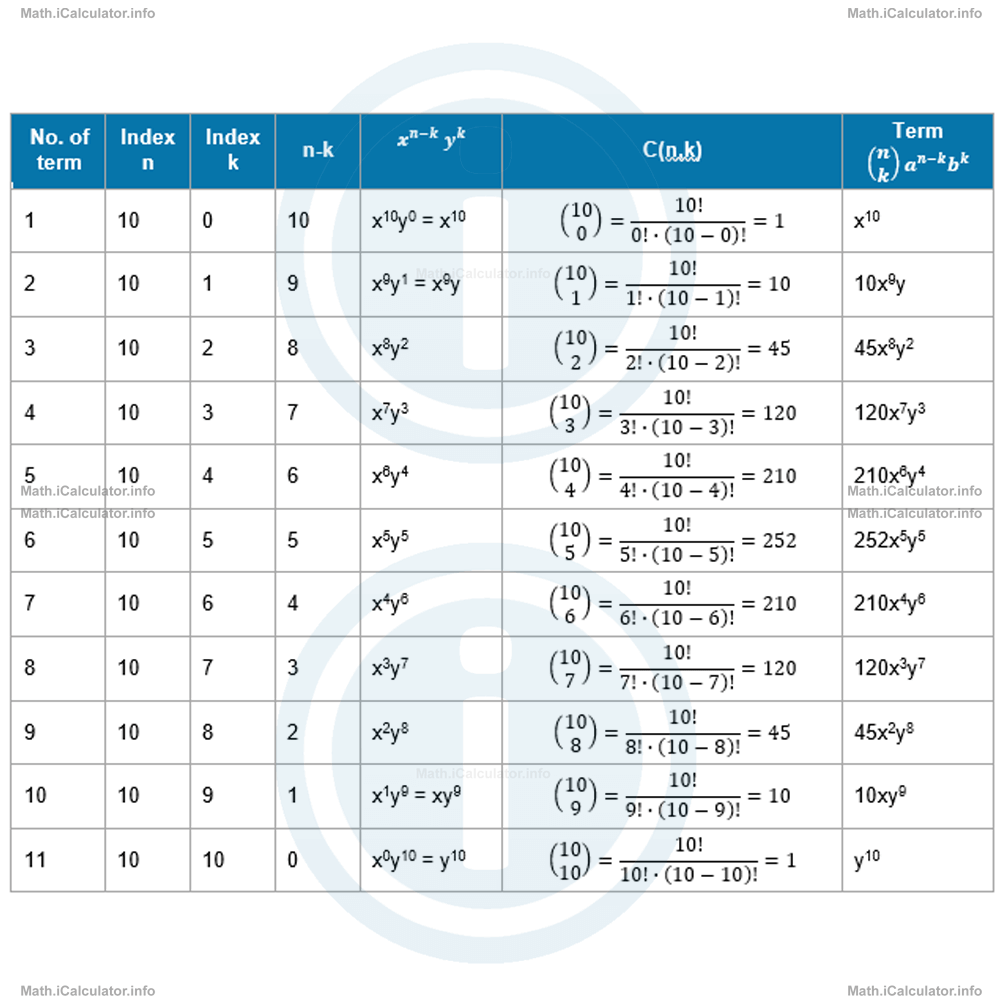
$Math Tutorials: Binomial Expansion and Coefficients Example$

Therefore, the expanded form of the binomial (x + y)¹⁰ is

(x + y)10 = x₁0 + 10x9y + 45x8y2 + 120x7y3 + 210x6y4 + 252x5y5 + 210x4y6 + 120x3y7 + 45x2y8 + 10xy9 + y10

We can generalize this approach to include all types of binomial expressions. For example, if we have to expand the binomial expression (3x - 2)⁵, first we express 3x = a and -2 = b, then we follow the procedure described in theory.

Example 4

Expand the following binomial expressions

(2x - 4)⁵
(1 - 3x)⁶

Solution 4

We replace 2x with a and -4 with b. Based on the Pascal's Triangle (or in the Binomial Coefficients Theorem if you wish), we obtain
(a + b)⁵ = a⁵ + 5a⁴ b + 10a³ b² + 10a² b³ + 5ab⁴ + b⁵
Now, we replace back a and b with the original terms. This, yields
(2x - 4)⁵ = (2x)⁵ + 5 ∙ (2x)⁴ ∙ (-4) + 10 ∙ (2x)³ ∙ (-4)² + 10 ∙ (2x)² ∙ (-4)³ + 5 ∙ (2x) ∙ (-4)⁴ + (-4)⁵
= 32x⁵ + 5 ∙ 16x⁴ ∙ (-4) + 10 ∙ 8x³ ∙ 16 + 10 ∙ 4x² ∙ (-64) + 5 ∙ (2x) ∙ 256 + (-1024)
= 32x⁵ - 320x⁴ + 1280x³ - 2560x² + 2560x - 1024
We replace 1 with a and -3x with b. Applying the Pascal's Triangle method (or the Binomial Coefficients Theorem if you wish), yields
(a + b)⁶ = a⁶ + 6a⁵ b + 15a⁴ b² + 20a³ b³ + 15a² b⁴ + 6ab⁵ + b⁶
Now, we replace back a and b with the original terms. This, yields
(1 - 3x)⁶ = 1⁶ + 6 ∙ 1⁵ ∙ (-3x) + 15 ∙ 1⁴ ∙ (-3x)² + 20 ∙ 1³ ∙ (-3x)³ + 15 ∙ 1² ∙ (-3x)⁴ + 6 ∙ 1 ∙ (-3x)⁵ + (-3x)⁶
= 1 + 6 ∙ 1 ∙ (-3x) + 15 ∙ 1 ∙ 9x² + 20 ∙ 1 ∙ (-27x³) + 15 ∙ 1 ∙ 81x⁴ + 6 ∙ 1 ∙ (-243x⁵) + 729x⁶
= 1 - 18x + 145x² - 540x³ + 1215x⁴ - 1458x⁵ + 729x⁶

More Binomial Expansion and Coefficients Lessons and Learning Resources

Sequences and Series Learning Material
Tutorial ID	Math Tutorial Title	Revision Notes	Revision Questions
12.3	Binomial Expansion and Coefficients
Lesson ID	Math Lesson Title	Lesson	Video Lesson
12.3.1	The Square and the Cube of a Binomial
12.3.2	How to Expand Binomials in Higher Powers
12.3.3	Using Pascal's Triangle
12.3.4	Working with Binomial Coefficients and the Limitation of Pascal's Triangle
12.3.5	The Binomial Coefficients Theorem
12.3.6	What is a Binomial when it is not in the Standard Form

Whats next?

Enjoy the "The Binomial Coefficients Theorem " math lesson? People who liked the "Binomial Expansion and Coefficients lesson found the following resources useful:

Binomial Coefficients Theory Feedback. Helps other - Leave a rating for this binomial coefficients theory (see below)
Sequences and Series Math tutorial: Binomial Expansion and Coefficients. Read the Binomial Expansion and Coefficients math tutorial and build your math knowledge of Sequences and Series
Sequences and Series Video tutorial: Binomial Expansion and Coefficients. Watch or listen to the Binomial Expansion and Coefficients video tutorial, a useful way to help you revise when travelling to and from school/college
Sequences and Series Revision Notes: Binomial Expansion and Coefficients. Print the notes so you can revise the key points covered in the math tutorial for Binomial Expansion and Coefficients
Sequences and Series Practice Questions: Binomial Expansion and Coefficients. Test and improve your knowledge of Binomial Expansion and Coefficients with example questins and answers
Check your calculations for Sequences and Series questions with our excellent Sequences and Series calculators which contain full equations and calculations clearly displayed line by line. See the Sequences and Series Calculators by iCalculator™ below.
Continuing learning sequences and series - read our next math tutorial: Infinite Series Explained

Help others Learning Math just like you