Math Lesson 15.8.3 - Calculating the Gradient of a Curve: Gradient of a quadratic function

Please provide a rating, it takes seconds and helps us to keep this resource free for all to use

Welcome to our Math lesson on Calculating the Gradient of a Curve: Gradient of a quadratic function, this is the third lesson of our suite of math lessons covering the topic of Gradient of Curves, you can find links to the other lessons within this tutorial and access additional Math learning resources below this lesson.

Calculating the Gradient of a Curve: Gradient of a quadratic function

The simplest quadratic function (also known as the parent quadratic function) is f(x) = x². Suppose we want to find the gradient at the point P(x₀, y₀). The procedure is the same as described in Lesson 2, Example 1 of this tutorial, i.e. we consider an interval Δx, Δy around the given point. However, instead of substituting numbers in the curve's formula, now we apply the analytic reasoning in the sense that first, we add the interval Δx to the variable x₀ in the original function, in the same way as we did in horizontal translations explained in the previous tutorial. In this way, given that the function at the point x₀ is written as f(x₀), we obtain

In this way, we have found the value of this function at the end of the interval chosen. Considering the point x₀ as the beginning of the interval, not as the middle of it (for convenience), allows us to find the change Δy in the y-coordinate of the function in the section considered. Thus, we have

As explained earlier, the gradient k is calculated by dividing the change in the y-coordinate by the change in the x-coordinate. In the specific case, we have

Now, since the change in the x-coordinate Δx is very small compared to the value of x₀, the Δx² term is even smaller (a number smaller than 1 when raised in square gives an even smaller number), we can neglect this term (Δx₀). In this way, for the gradient k we obtain:

Simplifying up and down by Δx yields

The coordinate x₀ can be any x-coordinate chosen for this purpose. Therefore, the general formula for the gradient of f(x) = x² is

Let's prove the correctness of this formula by finding the gradient of the parent quadratic function in both ways described above and see whether the results obtained are the same or not.

Example 2

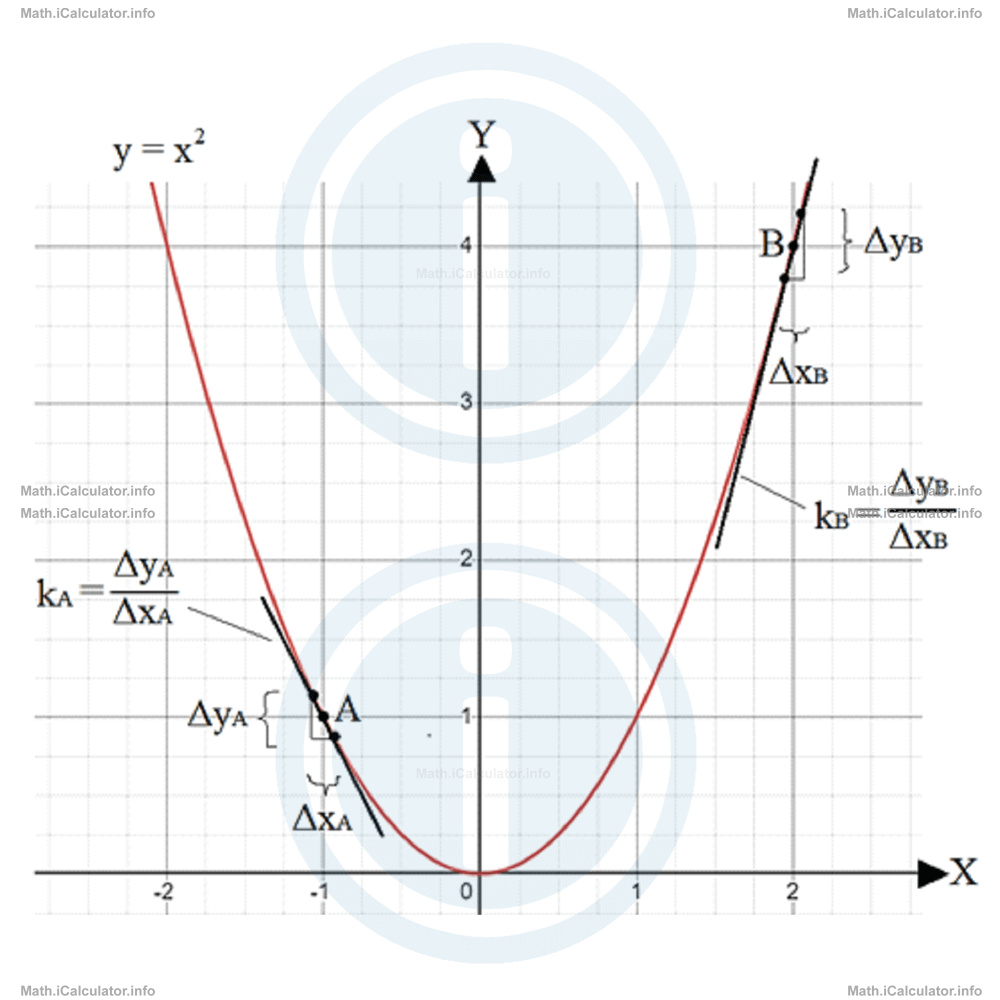
Calculate the gradient of y = x² at points A and B where x_A = -1 and x_B = 2. Then, plot the graph and show the relevant information on it.

Solution 2

Let's begin with the first method, i.e. by picking two values around each of the given points. Thus, for point A we choose x₁ = -1.1 and x² = -0.9. The corresponding y-values are

and

Hence, the gradient's value at point A is

The same procedure is followed with point B as well. We choose x₁ = 1.9 and x² = 2.1. Therefore, the corresponding y-values are

and

Hence, the gradient's value at point B is

Now, let's confirm the above results by means of the formula found in theory. Thus, since the gradient of the parent quadratic function f(x) = x² is k = 2x, we obtain for the gradients at points A and B

and

In this way, we obtained the same results as before, but in a much shorter way.

The figure below shows the graph including the two points A and B and the tangent lines at these points.

If the quadratic function f(x) contains more than one term, i.e. when it is expressed as a polynomial of the general form

then, the gradient's formula is obtained by considering each term separately. Thus, we have the following separate gradients:

1. Since the gradient of f(x) = x² is k = 2x, then the gradient of f(x) = ax² is k = 2ax. This is because f(x) = x² represents a special case of f(x) = ax² where a = 1.
2. Since the gradient of f(x) = bx is k = b (because this part represents a linear function where the gradient is equal to the coefficient preceding the variable), and
3. Since the gradient of f(x) = c is k = 0 because this is a constant function and its graph is horizontal (always at y = c), i.e. it has no inclination and therefore a zero gradient, then the gradient k of the quadratic function
   f(x) = ax² + bx + c
   is
   k = 2ax + b

Example 3

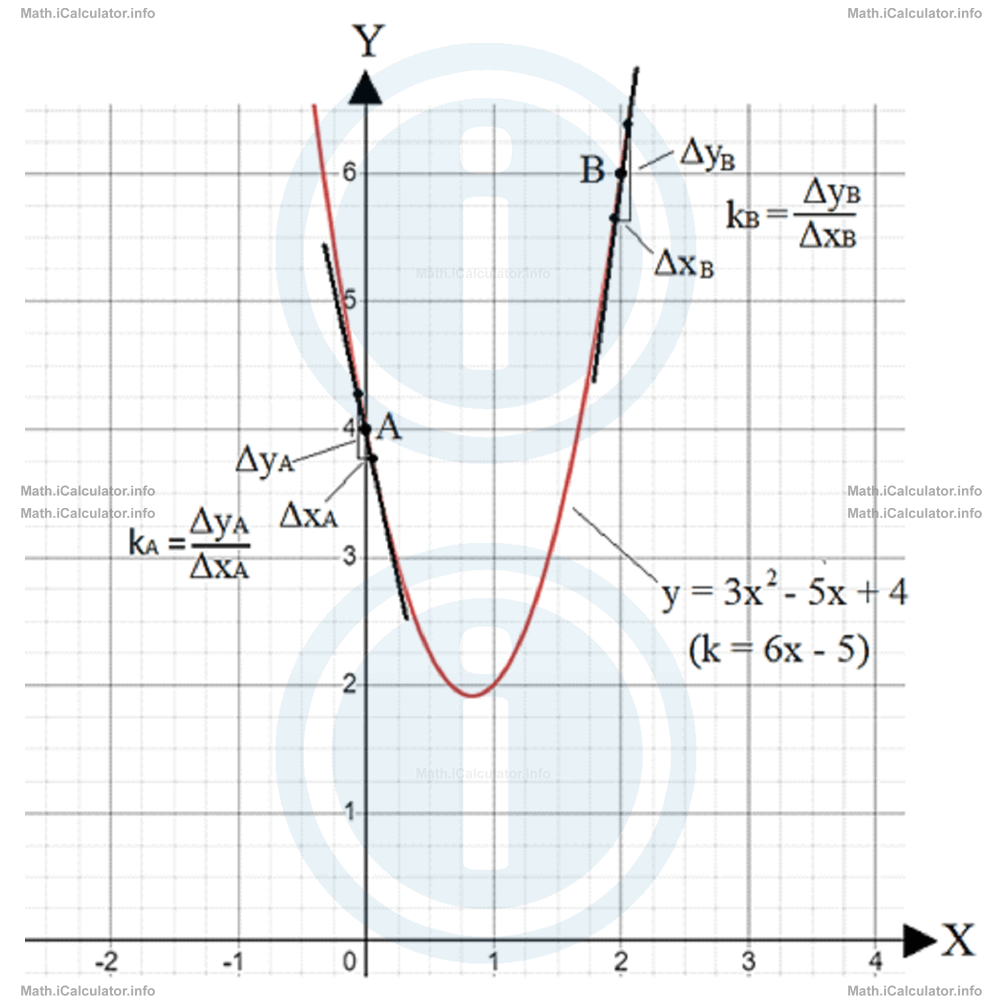
1. Find the general formula for the gradient of the function
   f(x) = 3x² - 5x + 4
2. Find the gradient's value for x = 0 and x = 6.
3. Confirm the results obtained in (b) using the first method, i.e. finding the gradient by substituting in the original function a couple of values around the given points.
4. Show the relevant info on the graph.

Solution 3

1. This function is quadratic, having a general formula f(x) = ax² + bc + c. In the specific case, we have a = 3, b = -5 and c = 4.
   From theory, we know that the gradient of a quadratic function has the general formula
   k = 2ax + b
   Hence, substituting the known values yields,
   k = 2 ∙ 3x - 5
   k = 6x - 5
2. For x = 0, the gradient k is
   k = 6x - 5
   = 6 ∙ 0 - 5
   = 0 - 5
   = -5
   This means at the point of the graph with horizontal coordinate x = 0 the y-coordinate of the graph decreases 5 times faster than the increase in the corresponding x-coordinate. On the other hand, for x = 2 the gradient k is
   k = 6x - 5
   = 6 ∙ 2 - 5
   = 12 - 5
   = 7
3. Now, we will find the gradient's value in the two given points by substituting values very close to the given points in the original function. (Beware to substitute these values in the original function, not in the gradient's formula.) Thus, for the first point (say, 'point A') with horizontal coordinate x_A = 0, we take two surrounding values x₁ = -0.1 and x² = 0.1 and calculate the corresponding y-values:
   y₁ = a ∙ x²₁ + b ∙ x₁ + c
   = 3 ∙ (-0.1)²-5 ∙ (-0.1) + 4
   = 3 ∙ 0.01-5 ∙ (-0.1) + 4
   = 0.03 + 0.5 + 4
   = 4.53
   and
   y₂ = a ∙ x²₂ + b ∙ x₂ + c
   = 3 ∙ (0.1)² - 5 ∙ (0.1) + 4
   = 3 ∙ 0.01 - 5 ∙ (0.1) + 4
   = 0.03 - 0.5 + 4
   = 3.53
   Therefore, the gradient k at point A is
   k_A = y₂ - y₁/x₂ - x₁
   = 3.53 - 4.53/0.1-(-0.1)
   = -1/0.1 + 0.1
   = -1/0.2
   = -5
   This is the same result as the one obtained at (b) for the gradient's value at the given point.
   Likewise, for x = 2 (say point B), we choose x₁ = 1.9 and x² = 2.1. Hence, the corresponding y-values are:
   y₁ = a ∙ x²₁ + b ∙ x₁ + c
   = 3 ∙ (1.9)² - 5 ∙ (1.9) + 4
   = 3 ∙ 3.61 - 5 ∙ 1.9 + 4
   = 10.83 - 9.5 + 4
   = 5.33
   and
   y₂ = a ∙ x²₂ + b ∙ x₂ + c
   = 3 ∙ (2.1)² - 5 ∙ (6.1) + 4
   = 3 ∙ 4.41 - 5 ∙ 2.1 + 4
   = 13.23 - 10.5 + 4
   = 6.73
   Therefore, the gradient k at point B is
   k_B = y₂ - y₁/x₂ - x₁
   = 6.73 - 5.33/2.1 - 1.9
   = 1.4/0.2
   = 7
   Again, this is the same result as the one obtained at (b) for the gradient's value at the given point.
4. The graph below shows all the findings in the previous points of this solution.

You have reached the end of Math lesson 15.8.3 Calculating the Gradient of a Curve: Gradient of a quadratic function. There are 4 lessons in this physics tutorial covering Gradient of Curves, you can access all the lessons from this tutorial below.

More Gradient of Curves Lessons and Learning Resources

Whats next?

Enjoy the "Calculating the Gradient of a Curve: Gradient of a quadratic function" math lesson? People who liked the "Gradient of Curves lesson found the following resources useful:

1. Quadratic Function Feedback. Helps other - Leave a rating for this quadratic function (see below)
2. Types of Graphs Math tutorial: Gradient of Curves. Read the Gradient of Curves math tutorial and build your math knowledge of Types of Graphs
3. Types of Graphs Revision Notes: Gradient of Curves. Print the notes so you can revise the key points covered in the math tutorial for Gradient of Curves
4. Types of Graphs Practice Questions: Gradient of Curves. Test and improve your knowledge of Gradient of Curves with example questins and answers
5. Check your calculations for Types of Graphs questions with our excellent Types of Graphs calculators which contain full equations and calculations clearly displayed line by line. See the Types of Graphs Calculators by iCalculator™ below.
6. Continuing learning types of graphs - read our next math tutorial: Quadratic Graphs Part One

Help others Learning Math just like you

Please provide a rating, it takes seconds and helps us to keep this resource free for all to use

We hope you found this Math tutorial "Gradient of Curves" useful. If you did it would be great if you could spare the time to rate this math tutorial (simply click on the number of stars that match your assessment of this math learning aide) and/or share on social media, this helps us identify popular tutorials and calculators and expand our free learning resources to support our users around the world have free access to expand their knowledge of math and other disciplines.

Types of Graphs Calculators by iCalculator™