Math Lesson 16.3.4 - Exponential Function

Please provide a rating, it takes seconds and helps us to keep this resource free for all to use

Welcome to our Math lesson on Exponential Function, this is the fourth lesson of our suite of math lessons covering the topic of Basic Functions, you can find links to the other lessons within this tutorial and access additional Math learning resources below this lesson.

Exponential Function

An exponential function has the general form

where a and m are coefficients, b is the base and c is a constant.

The base b is often the Euler's number 'e'. in this way, we obtain a special exponential function of the general form

For example,

is an exponential function where the base is e = 2.718 (We explained in previous chapters that Euler number is an infinite series of fractions where the numerator of all fractions is 1, while the denominator is n! where n is the number a certain term occupies in the series.

Again, in such functions, the domain is unlimited, as the independent variable x can take any value. The range, however, here is limited as, for example, if the base is positive the exponential part cannot be negative. Therefore, the function cannot be smaller than the constant c. Therefore, such functions have a minimum value of c. On the other hand, if the base is negative, the function f(x) can take a negative value for odd values of the index and a positive value for even indices, so the graph is a set of individual points not connected through a solid line.

As for the gradient, minimum, maximum, etc., the procedure is similar as in the functions discussed earlier.

Example 4

In the exponential function

find:

1. Domain and range.
2. The x-and y-intercept(s).
3. The gradient at x = 1 given that the formula for the gradient of an exponential function f(x) = ax is m = ax · ln a.
4. The equation of the tangent line at this point (at x = 1).
5. Plot the graph of the function f(x) and that of the tangent line t(x) at x = 1.

Solution 4

1. There are no restrictions on the possible choices for the independent variable x, so the domain D is practically the set of real numbers R (D = R).
   As for the range R, it is obvious that there is no maximum limit for the values of f(x) but only a minimum limit for negative values of x. Thus, if the variable x becomes more negative, the value of 2x becomes smaller and smaller, so it comes to a point where this part of the expression becomes zero (for x pointing towards minus infinity). Therefore, the minimum value of this function is -1, because this number is subtracted from the exponential part of the original function. Hence, we have R = [-1, + ∞).
2. The x-intercept is obtained for f(x) = 0. Thus,
   f(x) = 1/5 ∙ 2^{x - 1}
   0 = 1/5 ∙ 2^{x - 1}
   1 = 1/5 ∙ 2^x
   2^x = 5
   ln₂ 2^x = ln₂ 5
   x = ln₂ 5
   x = ln 5/ln 2
   x = 1.6/0.7
   x = 2.322
   
   Therefore, the x-intercept is at (2.322, 0).
   On the other hand, the y-intercept is obtained for x = 0. Thus,
   f(0) = 1/5 ∙ 2^{0 - 1}
   = 1/5 ∙ 1 - 1
   = 1/5 - 1
   = 1/5 - 5/5
   = -4/5
   = -0.8
   Hence, the y-intercept is at (0, -0.8).
3. Since the gradient of f(x) = ax is m = ax ln a, we obtain for the gradient of the given function (where a = 2)
   m = 1/5 ∙ 2^x ∙ ln⁡2
   Thus, at x = 1, we have
   m(1) = 1/5 ∙ 2¹ ∙ ln⁡2
   = 1/5 ∙ 2 ∙ ln2 = 2/5 ∙ 0.693
   = 0.2772
4. The equation of the tangent line with f(x) at x = 1 is
   y = mx + n
   where m is the gradient. In the specific case we have
   y = 0.2772 ∙ 1 + n
   y = 0.2772 + n
   Since f(x) and the tangent line have the same coordinates at the point of tangency, we must find f(1) in the original function, which corresponds to the y-value in the point of tangency. Thus,
   f(1) = 1/5 ∙ 2¹ - 1
   = 1/5 ∙ 2 - 1
   = 2/5 - 5/5
   = -3/5
   = -0.6
   Therefore, the constant n of the tangent line is
   -0.6 = 0.2772 + n
   n = -0.6 - 0.2772
   = -0.8772
   Hence, the equation of the tangent line to f(x) at x = 1 is
   y = 0.2772x - 0.8772
5. We can plot the graph based on the above findings. Thus, all what we know from the previous points is that the graph does not extend below y = -1 (which is a horizontal asymptote for the graph). This means the graph approaches y = -1 but does not touch it. In addition, A(2.322, 0) is the x-intercept while B(0, -0.8) is the y-intercept of the graph. Another point that belongs to the graph is the point of tangency with the line discussed in (d). We call this point C(1, -0.6).
   We may find other two optional points aside from those given above to make the graph more accurate. For example, for x = -4, we have
   f(-4) = 1/5 ∙ 2_-4 - 1
   = 1/5 ∙ 1/16-1
   = 1/80 - 1
   = 1/80 - 80/80
   = -79/80
   = -0.988
   Thus, another point of the graph is D(-4, -0.988).
   Let's take another point on the right side. For example, for x = 4 we have
   f(4) = 1/5 ∙ 2₄ - 1
   = 1/5 ∙ 16 - 1
   = 16/5 - 5/5
   = 11/5
   = 2.2
   Hence, point E(4, 2.2) is also a point of the graph. Inserting all the above points (including the tangent line) and connecting them smoothly, yields the following figure:

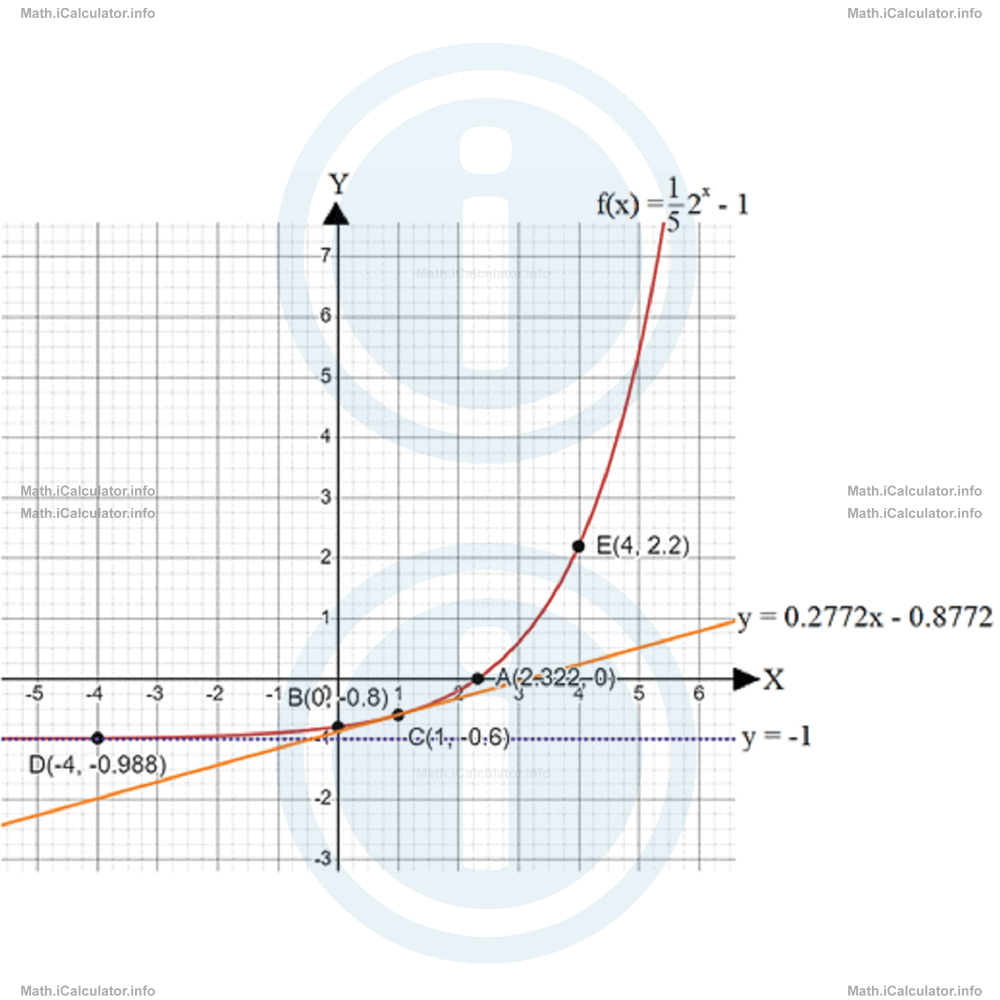
You have reached the end of Math lesson 16.3.4 Exponential Function. There are 8 lessons in this physics tutorial covering Basic Functions, you can access all the lessons from this tutorial below.

More Basic Functions Lessons and Learning Resources

Whats next?

Enjoy the "Exponential Function" math lesson? People who liked the "Basic Functions lesson found the following resources useful:

1. Exponential Feedback. Helps other - Leave a rating for this exponential (see below)
2. Functions Math tutorial: Basic Functions. Read the Basic Functions math tutorial and build your math knowledge of Functions
3. Functions Revision Notes: Basic Functions. Print the notes so you can revise the key points covered in the math tutorial for Basic Functions
4. Functions Practice Questions: Basic Functions. Test and improve your knowledge of Basic Functions with example questins and answers
5. Check your calculations for Functions questions with our excellent Functions calculators which contain full equations and calculations clearly displayed line by line. See the Functions Calculators by iCalculator™ below.
6. Continuing learning functions - read our next math tutorial: Composite Functions

Help others Learning Math just like you

Please provide a rating, it takes seconds and helps us to keep this resource free for all to use

We hope you found this Math tutorial "Basic Functions" useful. If you did it would be great if you could spare the time to rate this math tutorial (simply click on the number of stars that match your assessment of this math learning aide) and/or share on social media, this helps us identify popular tutorials and calculators and expand our free learning resources to support our users around the world have free access to expand their knowledge of math and other disciplines.

Functions Calculators by iCalculator™