Math Lesson 16.3.2 - Quadratic Functions

Please provide a rating, it takes seconds and helps us to keep this resource free for all to use

Welcome to our Math lesson on Quadratic Functions, this is the second lesson of our suite of math lessons covering the topic of Basic Functions, you can find links to the other lessons within this tutorial and access additional Math learning resources below this lesson.

Quadratic Functions

From previous chapters, it is known that quadratic functions have a general form

where a and b are coefficients and c is a constant (all of them are numbers), while x is the independent variable of the function.

The domain, codomain and range of a quadratic function are all unlimited unless the restrictions are explicitly stated in the clues. This is because this function has no square roots, logarithms, trigonometric elements, fractions, etc., which may bring restrictions in the allowed values.

The graph of a quadratic function is a parabola. The coefficient a of the quadratic function tells us what the orientation of the parabola is. Thus, if a > 0 the arms of the parabola are upwards; the graph of the quadratic function indicated by this parabola has a minimum at V(-b/2a, -Δ/4a), where Δ = b2 - 4ac is the discriminant of the corresponding quadratic equation f(x) = 0.

On the other hand, if the coefficient a of the parabola is negative (a < 0), the arms of the parabola are downwards; the graph of the quadratic function indicated by this parabola has a maximum at V(-b/2a, -Δ/4a). The x-coordinate of the vertex is also the equation of the symmetry line that divides the quadratic function graph into two equal halves.

The sign of the discriminant Δ also tells us a lot of useful info about the number of x-intercepts of the graph. These intercepts are called roots when dealing with the corresponding quadratic equation ax^x + bx + c = 0 or zeroes when dealing only with the quadratic polynomial ax^x + bx + c. Thus, if Δ > 0, the graph of f(x) = ax^x + bx + c has two x-intercepts at

This means the graph intercepts the horizontal axis at two points: A(x¹, 0) and B(x^x, 0).

On the other hand, if the discriminant Δ is zero, the parabola has a single contact point with the horizontal axis, at the vertex V. If the discriminant is negative, the parabola graph has no intercept points with the horizontal axis.

Given that a parabola is a kind of curve, we need to know more than the above three points to sketch the graph. Another point we can easily find is the y-intercept, which has the x-coordinate equal to zero. The corresponding f(x) for x = 0 is

Therefore, the fourth point (say point C) identified on the parabola is at C(0, c).

We have also used the symmetrical point to C when plotting quadratic graphs given that the x-coordinate of the vertex acts as a midpoint for the x-coordinates of the points C and D. Thus, from the segment midpoint formula

Thus,

The corresponding y-coordinate of point D is found by finding the value of the function for f(x) = f(xD). In other words, we substitute the x-coordinate of point D in the original function and find the corresponding y-value.

Another important element of quadratic functions is the gradient m, which - as explained in tutorial 15.8 - in quadratic functions has the formula m = 2ax + b. Since the gradient of a quadratic function varies depending on the x-value of the tangent point, the coefficient m of the tangent line to the quadratic graph y = mx + n is different at different points of the graph.

We have discussed all the above things in the previous chapters and in the previous tutorials of the graph. That's why we mentioned them very briefly. Let's illustrate everything discussed above with an example.

Example 2

For the quadratic function f(x) = 2x^x - 7x + 3 (x ∊ [-2, 7]) find the following:

1. Domain, range and codomain of this function.
2. Vertex of the parabola.
3. Intercepts of the graph with the two axes.
4. Gradient of this function.
5. Equation of the tangent line with the graph at x = 3.
6. Plot the graph of f(x) and show everything found in the previous points in the figure.

Solution 2

1. The domain D shows the set of the possible values the independent variable x can take. In this case, the domain is given in the clues. It is D = [-2, 7].
   As for the range R, it shows the minimum and maximum value of the function. We seek these two values in the y-coordinates of the domain endpoints and that of the vertex. Thus, for x = -2, we have
   f(-2) = 2 ∙ (-2)²-7 ∙ (-2) + 3
   = 2 ∙ 4 - 7 ∙ (-2) + 3
   = 8 + 14 + 3
   = 25
   and for x = 7, we have
   f(7) = 2 ∙ 7² - 7 ∙ 7 + 3
   = 2 ∙ 49 - 7 ∙ 7 + 3
   = 98 + 49 + 3
   = 52
   Now, let's find the y-coordinate of the vertex V. Since a = 2, b = -7 and c = 3, we have
   ∆ = b² - 4ac
   = (-7)² - 4 ∙ 2 ∙ 3
   = 49 - 24
   = 25
   Hence, the y-coordinate of the vertex is
   y_V = -∆/4a
   = -25/4 ∙ 2
   = -25/8
   Comparing the three y-values found above, it is clear that the range R extends between -25/8 (the minimum value) and 52 (the maximum value). Therefore, we have R = [-25/8, 52]. As for the codomain Y, it is the set of real numbers R, as the Y-axis contain real numbers. Thus, Y = R. (Again, be aware of the fact that the letter R is used twice but with a totally different meaning; once for representing the range and the other for the set of the real numbers that determine the codomain).
2. We have already found the y-coordinate of the vertex (y_V = -25/8). Now, we have to find the corresponding x-coordinate. Thus, given that
   x_V = -b/2a
   we obtain
   x_V = -(-7)/2 ∙ 2
   = 7/4
   Hence, the vertex is at V(7/4, -25/8). We can also write it as V(1.75, -3.125).
3. We can find the x-intercepts of this quadratic function by solving the equation f(x) = 0. Thus,
   2x²-7x + 3 = 0
   Since the discriminant is positive (we found earlier that Δ = 25), this equation has two roots:
   x₁ = -b - √∆/2a and x₂ = -b + √∆/2a
   The first root is
   x₁ = -(-7) - √25/2 ∙ 2
   = 7 - 5/4
   = 2/4
   = 1/2
   and the second root is
   x₂ = -(-7) + √25/2 ∙ 2
   = (7 + 5)/4
   = 12/4
   = 3
   Therefore, the two x-intercepts of the parabola are A(1/2, 0) and B(3, 0). We can also write them as A(0.5, 0) and B(3, 0).
4. It is known that the gradient of a quadratic function is m = 2ax + b. Given that a = 2 and b = -7, the gradient of this specific function is
   m = 2 ∙ 2 ∙ x + (-7)
   m = 4x - 7
5. At x = 3, the gradient is
   m = 4 ∙ 3 - 7
   = 12 - 7
   = 5
   The equation of the tangent at the given point (see tutorial 15.8) therefore is
   y = 5x + c
   Since x = 3, we have
   y = 5 ∙ 3 + c
   = 15 + c
   The constant c is found after finding the y-value at the point of tangency, i.e. after finding f(3) of the original function. This is because the original function meets with the tangent line at the given point, so both lines have the same x- and y-coordinate at that point. Thus,
   f(3) = 2 ∙ 3²-7 ∙ 3 + 3
   = 2 ∙ 9 - 7 ∙ 3 + 3
   = 18 - 21 + 3
   = 0
   Therefore, we have
   0 = 15 + c
   c = -15
   Hence, the equation of the tangent line to f(x) at x = 3 is
   y = 5x - 15
   Obviously, the tangency point will have a vertical coordinate equal to 0 because we found earlier that f(3) = 0. Therefore, the rightmost x-intercept B acts as a point of tangency as well.
6. The following figure shows the graph of the quadratic function f(x), the tangent line at x = 3, the x- and y-intercepts, and the parabola vertex. The function is shown with a solid line within the domain and with a dashed line outside it. The graph is a parabola with a minimum at V and with its arms extending upwards. 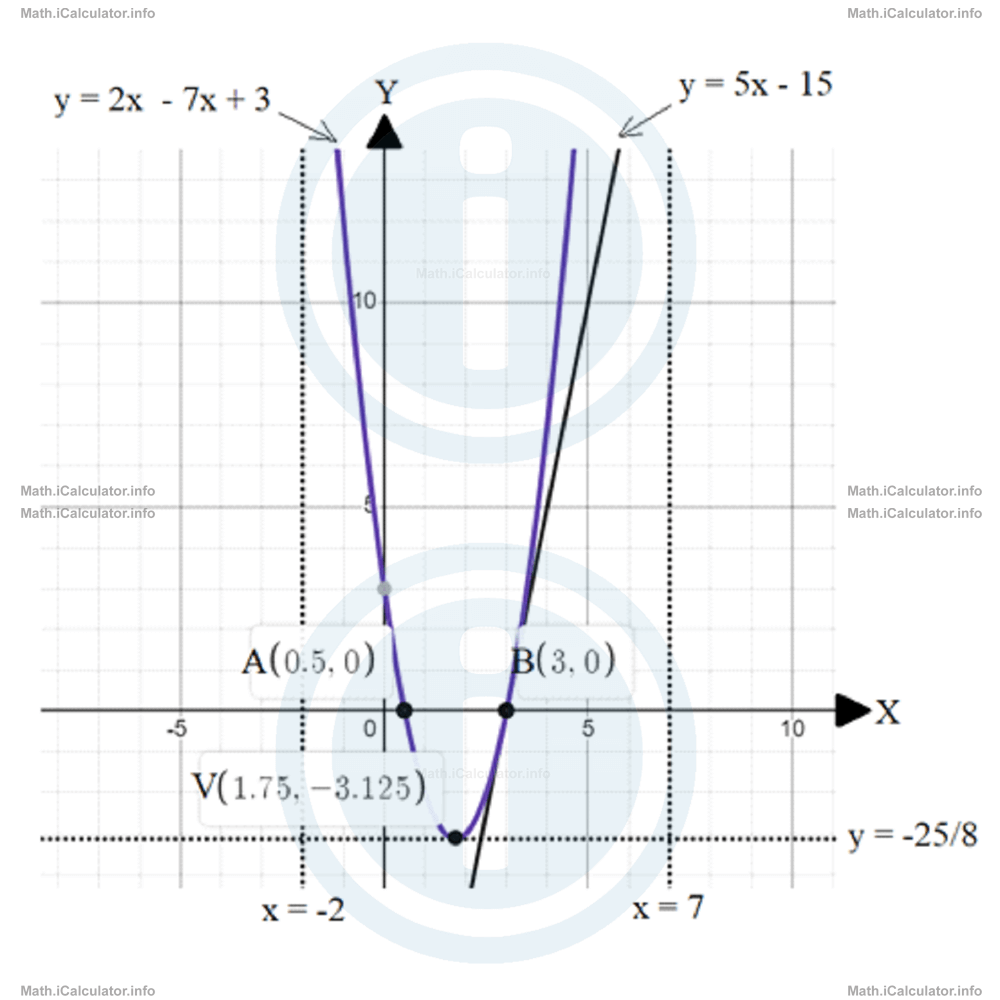We could not show the upper restriction determined by the range because the figure would become too large.

You have reached the end of Math lesson 16.3.2 Quadratic Functions. There are 8 lessons in this physics tutorial covering Basic Functions, you can access all the lessons from this tutorial below.

More Basic Functions Lessons and Learning Resources

Whats next?

Enjoy the "Quadratic Functions" math lesson? People who liked the "Basic Functions lesson found the following resources useful:

1. Quadratic Feedback. Helps other - Leave a rating for this quadratic (see below)
2. Functions Math tutorial: Basic Functions. Read the Basic Functions math tutorial and build your math knowledge of Functions
3. Functions Revision Notes: Basic Functions. Print the notes so you can revise the key points covered in the math tutorial for Basic Functions
4. Functions Practice Questions: Basic Functions. Test and improve your knowledge of Basic Functions with example questins and answers
5. Check your calculations for Functions questions with our excellent Functions calculators which contain full equations and calculations clearly displayed line by line. See the Functions Calculators by iCalculator™ below.
6. Continuing learning functions - read our next math tutorial: Composite Functions

Help others Learning Math just like you

Please provide a rating, it takes seconds and helps us to keep this resource free for all to use

We hope you found this Math tutorial "Basic Functions" useful. If you did it would be great if you could spare the time to rate this math tutorial (simply click on the number of stars that match your assessment of this math learning aide) and/or share on social media, this helps us identify popular tutorials and calculators and expand our free learning resources to support our users around the world have free access to expand their knowledge of math and other disciplines.

Functions Calculators by iCalculator™