Math Lesson 16.3.1 - Linear Functions

Please provide a rating, it takes seconds and helps us to keep this resource free for all to use

Welcome to our Math lesson on Linear Functions, this is the first lesson of our suite of math lessons covering the topic of Basic Functions, you can find links to the other lessons within this tutorial and access additional Math learning resources below this lesson.

Linear Functions

It is known that linear functions are one-to-one functions having a general form of

where the coefficient m represents the gradient of the line and n is the constant of the linear function. We explained earlier that such a function is linear because its graph is a straight line.

The gradient m is an indicator of the slope (steepness) of the graph in the sense that a linear graph is steeper for bigger coefficients m. On the other hand, the sign of m tells us whether the function is increasing or decreasing. Thus, if m is positive the function is increasing while if m is negative the function is decreasing. When m = 0, the function is constant [f(x) = n] and the graph is horizontal.

The method used to calculate the gradient is to consider two points A(x_A, y_A) and B(x_B, y_B) on the graph, where A is more on the left. Given the definition of gradient (change in the y-coordinate / change in the x-coordinate), the formula for calculation of the gradient of a linear function is

The x-intercept of the graph is obtained for y = 0. Hence,

Therefore, the x-intercept of a linear graph is at (-n/m, 0).

As for the y-intercept of a linear graph, it is obtained for x = 0. Hence, given that f(x) and y represent the same thing in a function, we have

Therefore, the y-intercept of a linear graph is at (0, n). Look at the figure below.

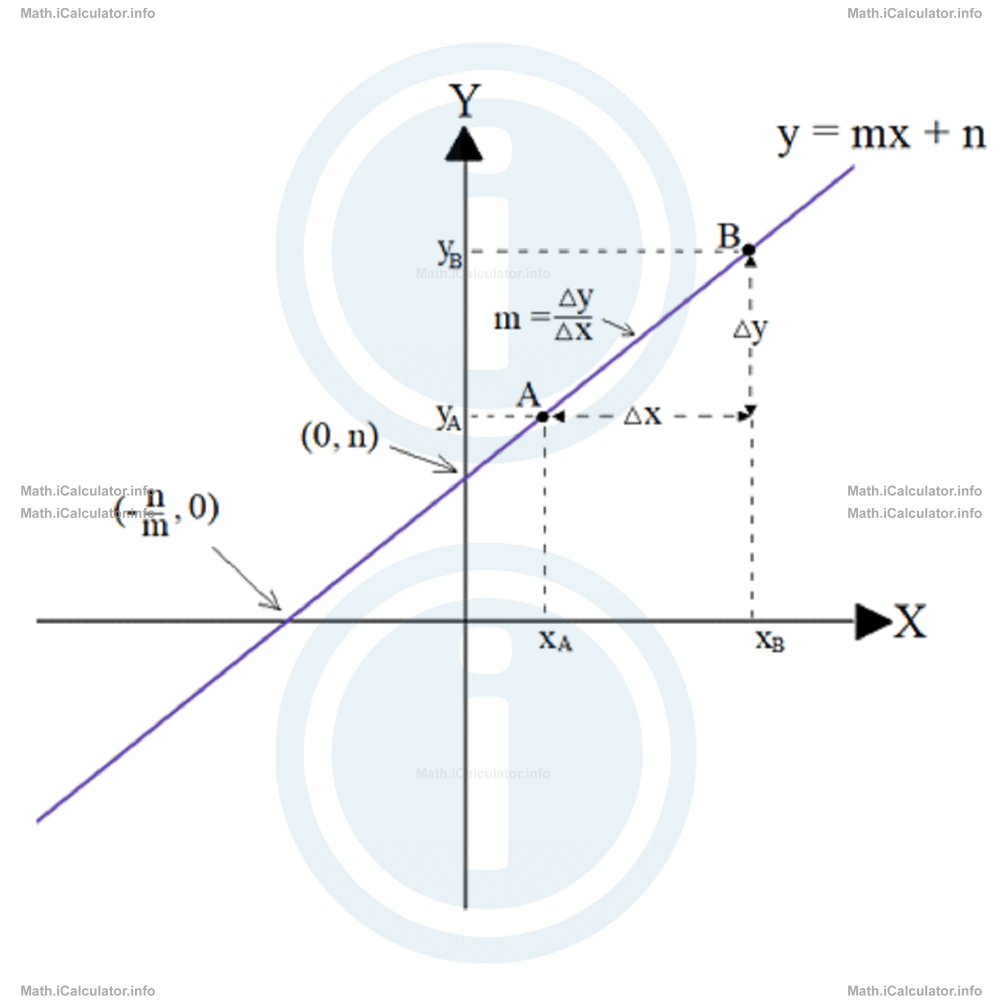
Another important thing to point out in linear function regards the domain D, codomain Y and range R. Thus if the set of the input values x is not restricted, then it corresponds to the set of real numbers; otherwise, it is determined by the segment or the interval specified in the initial conditions. As for the range, it is made up of the set of output values obtained by substituting the input values in the function's formula. Hence, if the domain of a linear function has no restrictions, the range will have no restrictions as well. On the other hand, if the domain is restricted within a segment or interval, so will occur to the range as well.

As for the codomain, it includes the range but may be wider in the sense that the codomain may contain more than just the output values obtained by substituting the input values in the function's formula. Let's see an example to clarify this point.

Example 1

Find the following for the function f(x) = -2x + 7 where x ∊ [-1, 4] and y ∊ [3, 18].

1. Domain D
2. Range R
3. Codomain Y
4. Gradient m
5. Intercepts of the graphs with the axes (if any) without plotting the graph
6. Plot the graph of this function

Solution 1

The domain D includes all input values of a function. In this case, we have D = X = [-1, 4].
1. The range R includes all values obtained by substituting the input values in the function. It is not possible to substitute all input values, as they are infinite in number but since the function is linear, we can consider only the boundary values x = -1 and x = 4 in this process. Thus, for x = -1 we have
   f(-1) = -2 ∙ (-1) + 7
   = 2 + 7
   = 9
   and
   f(4) = -2·4 + 7
   = -8 + 7
   = -1
   Therefore, the range R includes all values from -1 to 9. In symbols, we write R = [-1, 9].
2. The codomain Y includes all y-values given in the clues. Thus, we have Y = [-3, 18]. You can see that this set of values includes the range but it is wider.
3. The gradient m is the coefficient preceding the variable x in the function. Given that we are dealing with the function f(x) = -2x + 7, then the gradient is m = -2.
4. The x-intercepts is obtained for y = 0. Thus,
   0 = -2 ∙ x_int + 7
   2 ∙ x_int = 7
   x_int = 7/2
   Hence, the x-intercept is at (7/2, 0). The y-intercept is obtained for x = 0. Thus,
   y_int = -2 ∙ 0 + 7
   y_int = 0 + 7
   y_int = 7
   Hence, the y-intercept of the given linear function is at (0, 7).
5. It is a known fact that two points are sufficient to draw a straight line. We can use the x- and y-intercepts found at (d) to plot the graph of the function f(x) = -2x + 7. However, the graph must only be inside the rectangle obtained by the restrictions of the domain and range determined by the initial conditions of this function. We can show the part of the line that makes the function with a solid line and the rest of this linear function that extends outside the domain and range with a dashed line. Look at the figure below.

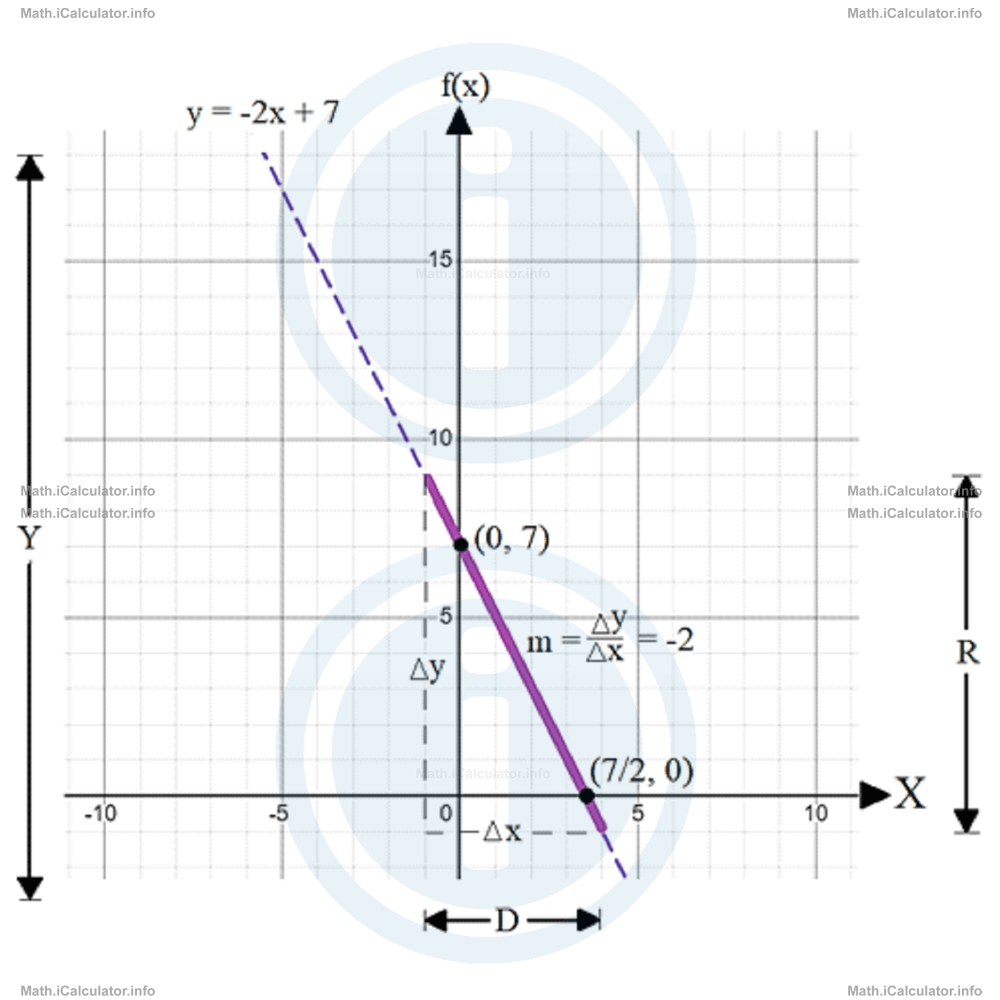
In the previous tutorials, we explained that a function is increasing if for any two points A and B (A is the leftmost, i.e. x_B > x_A), then f(B) > f(A). The graph line resulting from the increasing functions has a positive gradient. This means the graph goes up when moving from left to right.

On the other hand, a function is decreasing if for any two points A and B (A is the leftmost, i.e. x_B > x_A), then f(B) < f(A). The graph line resulting from the decreasing functions has a negative gradient. This means the graph goes down when moving from left to right. The function discussed in example 1 is decreasing as the graph is inclined down.

The graph in the above example is moving down, so the function f(x) represented by this graph is decreasing. The gradient of this function is negative; this means for every increase in the x-coordinate there is a decrease in the corresponding y-coordinate. Indeed, the x-coordinate has increased from 0 to 7/2 while the corresponding y-coordinate has decreased from 7 to 0.

When a linear function is neither increasing nor decreasing, it is constant.

You have reached the end of Math lesson 16.3.1 Linear Functions. There are 8 lessons in this physics tutorial covering Basic Functions, you can access all the lessons from this tutorial below.

More Basic Functions Lessons and Learning Resources

Whats next?

Enjoy the "Linear Functions" math lesson? People who liked the "Basic Functions lesson found the following resources useful:

1. Linear Feedback. Helps other - Leave a rating for this linear (see below)
2. Functions Math tutorial: Basic Functions. Read the Basic Functions math tutorial and build your math knowledge of Functions
3. Functions Revision Notes: Basic Functions. Print the notes so you can revise the key points covered in the math tutorial for Basic Functions
4. Functions Practice Questions: Basic Functions. Test and improve your knowledge of Basic Functions with example questins and answers
5. Check your calculations for Functions questions with our excellent Functions calculators which contain full equations and calculations clearly displayed line by line. See the Functions Calculators by iCalculator™ below.
6. Continuing learning functions - read our next math tutorial: Composite Functions

Help others Learning Math just like you

Please provide a rating, it takes seconds and helps us to keep this resource free for all to use

We hope you found this Math tutorial "Basic Functions" useful. If you did it would be great if you could spare the time to rate this math tutorial (simply click on the number of stars that match your assessment of this math learning aide) and/or share on social media, this helps us identify popular tutorials and calculators and expand our free learning resources to support our users around the world have free access to expand their knowledge of math and other disciplines.

Functions Calculators by iCalculator™